题目内容
【题目】有一座抛物线型拱桥,在正常水位时水面![]() 的宽为18米,拱顶
的宽为18米,拱顶![]() 离水面
离水面![]() 的距离
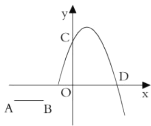
的距离![]() 为9米,建立如图所示的平面直角坐标系.
为9米,建立如图所示的平面直角坐标系.
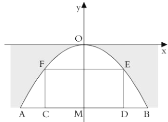
(1)求此抛物线的解析式;
(2)一艘货船在水面上的部分的横断面是矩形![]() .
.
①如果限定矩形的长![]() 为12米,那么要使船通过拱桥,矩形的高
为12米,那么要使船通过拱桥,矩形的高![]() 不能超过多少米?
不能超过多少米?
②若点![]() ,
,![]() 都在抛物线上,设
都在抛物线上,设![]() ,当
,当![]() 的值最大时,求矩形
的值最大时,求矩形![]() 的高.
的高.
【答案】(1)此抛物线的解析式为y=-![]() x2;(2)①要使船通过拱桥,矩形的高DE不能超过5米;②矩形CDEF的高为
x2;(2)①要使船通过拱桥,矩形的高DE不能超过5米;②矩形CDEF的高为![]() 米.
米.
【解析】
(1)根据题意设抛物线的解析式为y=ax2(a≠0).把已知坐标(9,-9)代入解析式求得a即可;
(2)①已知CD=12,把已知坐标代入函数关系式可求解;
②设DM=a米,可得EF=CD=2DM=2a米、DE=FC=9-![]() a2,根据L=EF+DE+CF求得L的值最大时a的值,代入DE=9-
a2,根据L=EF+DE+CF求得L的值最大时a的值,代入DE=9-![]() a2问题可解.
a2问题可解.
解:(1)根据题意,设抛物线解析式为:y=ax2,
将点B(9,-9)代入,得:81a=-9,
解得:a=-![]() ,
,
此抛物线的解析式为y=-![]() x2;
x2;
(2)①当x=6时,y=-![]() ×36=-4,
×36=-4,
∵9-4=5,
∴矩形的高DE不能超过5米,才能使船通过拱桥;要使船通过拱桥,矩形的高DE不能超过5米;
②设DM=a米,则EF=CD=2DM=2a米,
当x=a时,y=-![]() a2,
a2,
∴DE=FC=9-![]() a2,
a2,
则L=2a+2(9-![]() a2)=-
a2)=-![]() a2+2a+18=-
a2+2a+18=-![]() (a-
(a-![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L取得最大值,矩形CDEF的高为
时,L取得最大值,矩形CDEF的高为![]() 米
米

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目