题目内容
已知△ABC中，AB=8，AC=6，AD是中线，求AD的取值范围是________．
1＜AD＜7
分析：先作辅助线，延长AD至点E，使DE=AD，连接EC，先证明△ABD≌△ECD，在△AEC中，由三角形的三边关系定理得出答案．
解答：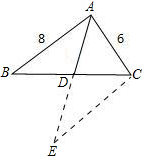
解：延长AD至点E，使DE=AD，连接EC，
∵BD=CD，DE=AD，∠ADB=∠EDC，
∴△ABD≌△ECD，∴CE=AB，
∵AB=8，AC=6，CE=8，
设AD=x，则AE=2x，
∴2＜2x＜14，
∴1＜x＜7，
∴1＜AD＜7．
点评：本题考查了三角形的三边关系定理：三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边．
分析：先作辅助线，延长AD至点E，使DE=AD，连接EC，先证明△ABD≌△ECD，在△AEC中，由三角形的三边关系定理得出答案．
解答：
解：延长AD至点E，使DE=AD，连接EC，∵BD=CD，DE=AD，∠ADB=∠EDC，
∴△ABD≌△ECD，∴CE=AB，
∵AB=8，AC=6，CE=8，
设AD=x，则AE=2x，
∴2＜2x＜14，
∴1＜x＜7，
∴1＜AD＜7．
点评：本题考查了三角形的三边关系定理：三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边．
练习册系列答案
相关题目
如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程证明△ABD≌△ACD的理由．
已知△ABC中，AB=AC，AD为BC边上的中线，BE为AC边上的高，
如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．
如图：已知△ABC中，AB=17cm，BC=30cm，BC边上的中线AD=8cm．求证：△ABC是等腰三角形．