题目内容
已知四边形的边长分别为a、b、c、d，且满足a2+b2+c2+d2=2ac+2bd，则此四边形的对角线具有性质：________．
对角线互相平分
分析：根据题中的等式可推出边的关系，从而可判断四边形为平行四边形，然后根据平行四边形对角线的性质即可得出答案．
解答：根据a2+b2+c2+d2=2ac+2bd，
整理得：（a-c）2+（b-d）2=0．
∴a=c，b=d，
∴此四边形是平行四边形，
∴平行四边形的对角线互相平分．
故答案为：对角线互相平分．
点评：本题考查了配方法的应用、平行四边形的判定及平行四边形对角线的性质，难度适中．
分析：根据题中的等式可推出边的关系，从而可判断四边形为平行四边形，然后根据平行四边形对角线的性质即可得出答案．
解答：根据a2+b2+c2+d2=2ac+2bd，
整理得：（a-c）2+（b-d）2=0．
∴a=c，b=d，
∴此四边形是平行四边形，
∴平行四边形的对角线互相平分．
故答案为：对角线互相平分．
点评：本题考查了配方法的应用、平行四边形的判定及平行四边形对角线的性质，难度适中．
练习册系列答案
相关题目
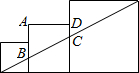已知三个边长分别为1，2，3的正方形如图排成一排，图中四边形ABCD的周长是