题目内容
若一次函数y=（m-2）x+1-m的函数值y随x的增加而减少，且函数图象与y轴交于x轴下方，则m的取值范围是
1＜m＜2
1＜m＜2
．分析：先根据一次函数y=（m-2）x+1-m的函数值y随x的增加而减少可知m-2＜0，再由函数图象与y轴交于x轴下方可知1-m＜0，进而可得出结论．
解答：解：∵一次函数y=（m-2）x+1-m的函数值y随x的增加而减少，
∴m-2＜0，解得m＜2；
∵函数图象与y轴交于x轴下方，
∴1-m＜0，解得m＞1，
∴m的取值范围是1＜m＜2．
故答案为：1＜m＜2．
∴m-2＜0，解得m＜2；
∵函数图象与y轴交于x轴下方，
∴1-m＜0，解得m＞1，
∴m的取值范围是1＜m＜2．
故答案为：1＜m＜2．
点评：本题考查的是一次函数的图象与性质，根据题意列出关于m的不等式是解答此题的关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
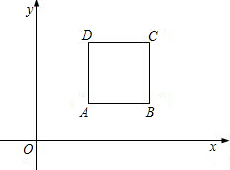如图，四边形ABCD是正方形，已知A（5，4），B（10，4）：