题目内容
定义:我们把三![]() 角形被一边中线分成的两个三角形叫做“友好三角形”
角形被一边中线分成的两个三角形叫做“友好三角形”
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等,
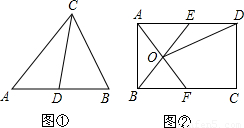
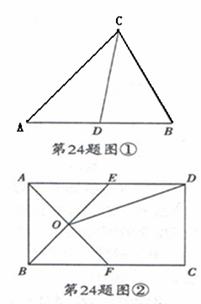
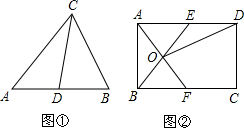
理解:如图①,在![]() 中,CD是AB边上的中线,那么
中,CD是AB边上的中线,那么![]() 和
和![]() 是“友好三角形”,并且
是“友好三角形”,并且![]() 。
。
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O,
(1) 求证: ![]() 和
和![]() 是“友好三角形”;
是“友好三角形”;
(2) 连接OD,若![]() 和
和![]() 是“友好三角形”,求四边形CDOF的面积,
是“友好三角形”,求四边形CDOF的面积,
探究:在![]() 中,
中,![]() ,AB=4,点D在线段AB上,连接CD,
,AB=4,点D在线段AB上,连接CD,![]() 和
和![]() 是“友好三角形”,将
是“友好三角形”,将![]() 沿CD所在直线翻折,得到
沿CD所在直线翻折,得到![]() 与
与![]() 重合部分的面积等于
重合部分的面积等于![]() 面积的
面积的![]() ,请直接写出
,请直接写出![]() 的面积。
的面积。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 (2013•沈阳)定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
(2013•沈阳)定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.

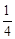 ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.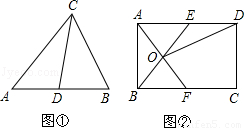
 ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.