题目内容
阅读下面的材料,并解答问题:问题1:已知正数,有下列命题若a+b=2,则
| ab |
| ab |
| 3 |
| 2 |
| ab |
根据以上三个命题所提供的规律猜想:若a+b=9,则
| ab |
以上规律可表示为a+b
| ab |
问题2:建造一个容积为8立方米,深2米的长方形无盖水池,池底和池壁的造价分别为每平方米120元和80元.
(1)设池长为x米,水池总造价为y(元),求y和x的函数关系式;
(2)应用“问题1”题中的规律,求水池的最低造价.
分析:问题1:根据以上三个命题所提供的规律猜想可得出结论.
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为
,y=480+320x+
.
(2)周长最短,正方形周长最短,a+b=2
,这样得出池壁面积为16米,进而算出总造价.
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为
| 4 |
| x |
| 1280 |
| x |
(2)周长最短,正方形周长最短,a+b=2
| ab |
解答:解:问题1:根据以上三个命题所提供的规律猜想可得:
;≥.
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为
,y=480+320x+
.
(2)底面积:8÷2=4平米,
周长最短为:8米(正方形周长最短),a+b=2
,
池壁面积:8×2=16平米,
总造价为:120×4+16×80=1760元.
| 9 |
| 2 |
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为
| 4 |
| x |
| 1280 |
| x |
(2)底面积:8÷2=4平米,
周长最短为:8米(正方形周长最短),a+b=2
| ab |
池壁面积:8×2=16平米,
总造价为:120×4+16×80=1760元.
点评:通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为a+b=n.则
≤
.
| ab |
| n |
| 2 |

练习册系列答案
相关题目
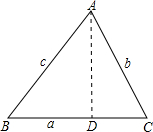 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.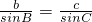
 过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明.
过点A作AD⊥BC,垂足为D,则在Rt△ABD和Rt△ACD中由正弦定义可完成证明. ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.
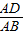 ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.

 ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.

 ,则AD=csinB
,则AD=csinB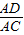 ,则AD=bsinC
,则AD=bsinC
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.