题目内容
如图,已知AB=3,BC=7,CD= .且AB⊥BC,∠BCD=135°.点M是线段BC上的一个动点,连接AM、DM.点M在运动过程中,
.且AB⊥BC,∠BCD=135°.点M是线段BC上的一个动点,连接AM、DM.点M在运动过程中,①当AM+DM的值最小时,BM= ;
②当AM2+DM2的值最小时,BM= .

【答案】分析:(1)延长AB到E,使BE=AB,连接ED交BC于M,连接AM,则此时AM+DM的值最小,过D作DF⊥BC交BC延长线于F,求出DF,根据相似求出BM即可;
(2)根据勾股定理得出AM2=AB2+BM2=32+x2,DM2=DF2+FM2=52+(5+7-x)2,相加即可求出答案.
解答:解:(1) 延长AB到E,使BE=AB,连接ED交BC于M,连接AM,则此时AM+DM的值最小,过D作DF⊥BC交BC延长线于F,
延长AB到E,使BE=AB,连接ED交BC于M,连接AM,则此时AM+DM的值最小,过D作DF⊥BC交BC延长线于F,
∵∠BCD=135°,
∴∠DCF=45°,
∵CD=5 ,
,
则CF=CD×cos45°=5,
DF=CF=5,
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
∴△BEM∽△FDM,
∴ =
= .
.
∴ =
= ,
,
∴BM= ,
,
(2)设BM=x,
在Rt△ABM中,AM2=AB2+BM2=32+x2,
∵在Rt△DFM中,DM2=DF2+FM2=52+(5+7-x)2,
∴AM2+DM2
=9+x2+25+(12-x)2
=2x2-24x+178
=2(x-6)2+106,
∵2>0,
∴AM2+DM2有最小值,当x=6时,最小值是106,
故答案为: ;6.
;6.
点评:本题考查了轴对称-最短路线问题,勾股定理,二次函数的最值,相似三角形的性质和判定,关键是找出符合条件的点,题目比较好.
(2)根据勾股定理得出AM2=AB2+BM2=32+x2,DM2=DF2+FM2=52+(5+7-x)2,相加即可求出答案.
解答:解:(1)
 延长AB到E,使BE=AB,连接ED交BC于M,连接AM,则此时AM+DM的值最小,过D作DF⊥BC交BC延长线于F,
延长AB到E,使BE=AB,连接ED交BC于M,连接AM,则此时AM+DM的值最小,过D作DF⊥BC交BC延长线于F,∵∠BCD=135°,
∴∠DCF=45°,
∵CD=5
 ,
,则CF=CD×cos45°=5,
DF=CF=5,
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
∴△BEM∽△FDM,
∴
 =
= .
.∴
 =
= ,
,∴BM=
 ,
,(2)设BM=x,
在Rt△ABM中,AM2=AB2+BM2=32+x2,
∵在Rt△DFM中,DM2=DF2+FM2=52+(5+7-x)2,
∴AM2+DM2
=9+x2+25+(12-x)2
=2x2-24x+178
=2(x-6)2+106,
∵2>0,
∴AM2+DM2有最小值,当x=6时,最小值是106,
故答案为:
 ;6.
;6.点评:本题考查了轴对称-最短路线问题,勾股定理,二次函数的最值,相似三角形的性质和判定,关键是找出符合条件的点,题目比较好.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由. 17、(保留作图痕迹)如图,已知AB=DC.
17、(保留作图痕迹)如图,已知AB=DC.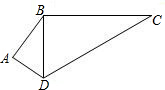 如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由.
如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由. 如图:已知AB∥DE,点C是AE的中点,
如图:已知AB∥DE,点C是AE的中点, 如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.
如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.