题目内容

如图所示，一次函数y=x+b与反比例函数y= $数学公式$ 的图象相交于A，B两点，若已知一个交点A（3，2），则另一个交点B的坐标为

A.
（3，-2）
B.
（-3，-2）
C.
（2，3）
D.
（-2，-3）

D
分析：因为A在函数y=x+b和 $\text{[math]}$ 上，则点A的坐标适合这两个函数关系，从而求出b和k，然后联立这两函数求出交点坐标．
解答：把A（3，2）代入y=x+b与y= $\text{[math]}$ 中，
得：b=-1，k=6，
所以y=x-1，y= $\text{[math]}$ ，
联立 $\text{[math]}$
得 $\text{[math]}$ 或 $\text{[math]}$ ，
所以B点坐标是（-2，-3）．
故选D．
点评：解答本题的关键是要理解两函数交点和方程组的解的对应关系．同时同学们要掌握解方程组的方法．

练习册系列答案

课时全练讲练测达标100分系列答案

点金训练精讲巧练系列答案

火线100天中考滚动复习法系列答案

新课堂同步学习与探究系列答案

优等生单元期末冲刺100分系列答案

绿色指标自我提升系列答案

支点系列答案

新课程资源与学案系列答案

初中复习与能力训练系列答案

习题精选系列答案

相关题目

博物馆每周都吸引大量中外游客前来参观．如果游客过多，对馆中的珍贵文物会产生不利影响．但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入．因此，博物馆采取了涨浮门票价格的方法来控制参观人数，在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系，在这样的情况下，如果

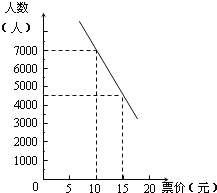确保每周4万元的门票收入，那么每周应限定参观人数是多少门票价格应是多少元？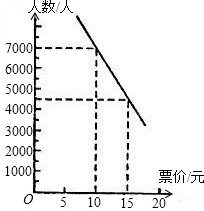

某博物馆每周都有大量中外游客前来参观，如果游客过多，则不利于博物馆中的一些珍贵文物的保存，但又需要一定量的门票收入用于解决文物的保存，保护等费用问题，因此博物馆通过浮动门票价格的方法来控制参观人数，调查统计发现，每周参观的人数与票价之间的关系可近似地看成如图所示的一次函数关系．
（1）求图中一次函数的解析式；
（2）为确保每周4万元的门票收入，则门票价格应定为多少元？

国家为了节能减排，计划对购买太阳能热水器进行政府补贴，为确定每购买一台太阳能热水器的政府补贴额，对某太阳能热水器专卖店的降价促销情况进行调研发现：销售额y（台）与每台降价额x（元）满足如图①所示的一次函数关系，销售每台太阳能热水器的收益z（元）与x满足如图②所示的一次函数关系．

（1）在未降价促销前，该专卖店销售太阳能热水器的总收益额为

元；
（2）在降价促销后，求出该专卖店的销售额y、每台收益z与每台降价x的函数关系式；
（3）当每台降价额x定为多少时，该专卖店销售太阳能热水器的总收益w（元）最大？并求出总收益w的最大值．

某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，则旅客可携带的免费行李的最大质量为

某航空公司规定，旅客乘机所携带行李的运费y（元）与其质量x（kg）由（如图所示）一次函数确定，那么旅客可携带的免费行李的最大质量为（　　）