题目内容
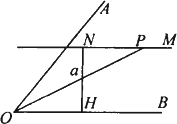
如图,已知AOB为一条直线,OC为任一条射线,OD平分∠BOC,OE平分∠AOC,试判断OD与OE的位置关系,并加以说明。

解:OD⊥OE
理由如下:因为OD平分∠BOC,
所以∠COD= ∠BOC
∠BOC
同理∠COE= ∠AOC
∠AOC
因为∠AOC+∠BOC=180°,
所以∠EOD=∠COE+∠COD= (∠AOC+∠BOC)=
(∠AOC+∠BOC)=  ×180°=90°
×180°=90°
所以OE⊥OD。
理由如下:因为OD平分∠BOC,
所以∠COD=
 ∠BOC
∠BOC同理∠COE=
 ∠AOC
∠AOC因为∠AOC+∠BOC=180°,
所以∠EOD=∠COE+∠COD=
 (∠AOC+∠BOC)=
(∠AOC+∠BOC)=  ×180°=90°
×180°=90°所以OE⊥OD。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 拿起画图工具,耐心画一画如图,已知∠AOB.
拿起画图工具,耐心画一画如图,已知∠AOB.