题目内容
有两棵相距8米的大树,一棵高12米,一棵高16米,一只小鸟从一棵树顶飞到另一棵树顶,至少需飞________米.
4
分析:根据“两点之间线段最短”,飞行的最短路线为沿着两棵树的最高点直线飞行,与两棵树的间距和高出树的长度,可构成直角三角形,用勾股定理可求出飞行的最少距离.
解答: 解:设两棵树的间距为AB,树的高出部分为BC,则飞行的最少距离为AC.
解:设两棵树的间距为AB,树的高出部分为BC,则飞行的最少距离为AC.
∵BC=16-12=4m,AB=8m
∴AC= =
=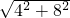 =
= .
.
点评:本题的关键是读懂题意,将实际问题转化为数学问题,运用勾股定理求解.

分析:根据“两点之间线段最短”,飞行的最短路线为沿着两棵树的最高点直线飞行,与两棵树的间距和高出树的长度,可构成直角三角形,用勾股定理可求出飞行的最少距离.
解答:
 解:设两棵树的间距为AB,树的高出部分为BC,则飞行的最少距离为AC.
解:设两棵树的间距为AB,树的高出部分为BC,则飞行的最少距离为AC.∵BC=16-12=4m,AB=8m
∴AC=
 =
=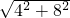 =
= .
.点评:本题的关键是读懂题意,将实际问题转化为数学问题,运用勾股定理求解.

练习册系列答案
相关题目
 如图,某一平地上,有一棵树高13米的大树,一棵树高8米的小树,两树之间相距12米.今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?
如图,某一平地上,有一棵树高13米的大树,一棵树高8米的小树,两树之间相距12米.今一只小鸟在其中一棵树的树梢上,要飞到另一棵树的树梢上,问它飞行的最短距离是多少?
