题目内容
抛物线y=ax2-(a+
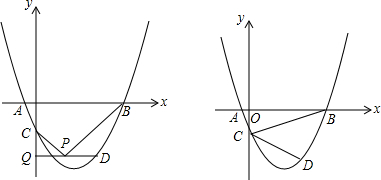
)x+b过点D(2,-2),交x轴分别于A、B两点(A在B的左侧),交y轴于C,且直线y=kx-1过C、D.
(1)求抛物线的解析式;
(2)过D作DQ⊥y轴于点Q,将抛物线沿x轴向左平移m个单位交线段DQ于点P(不与Q、D重合),当BP⊥CP时,求m的值;
(3)将△BCD绕点D逆时针旋转,使两条射线DB、DC分别交x、y轴于M、N,是否存在这样的点M、N,使
=
?若存在,求M、N的坐标;若不存在,请说明理由.
| 4 |
| 3 |
(1)求抛物线的解析式;
(2)过D作DQ⊥y轴于点Q,将抛物线沿x轴向左平移m个单位交线段DQ于点P(不与Q、D重合),当BP⊥CP时,求m的值;
(3)将△BCD绕点D逆时针旋转,使两条射线DB、DC分别交x、y轴于M、N,是否存在这样的点M、N,使
| OM |
| ON |
| 3 |
| 5 |

分析:(1)利用直线解析式求出点C的坐标,再把点C、D的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答;
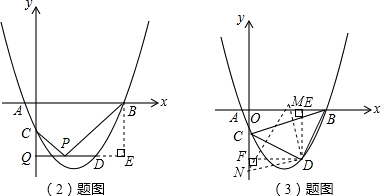
(2)过点B作BE⊥DQ交QD的延长线于E,然后求出△PCQ和△BPE相似,根据相似三角形对应边成比例列式求出PQ的长,再根据m=DQ-PQ计算即可得解;
(3)利用勾股定理列式求出BC、BD、CD,再利用勾股定理逆定理求出∠BDC=90°,过点D作DE⊥x轴于E,作DF⊥y轴于F,根据同角的余角相等求出∠MDE=∠NDF,再利用“角角边”证明△MDE和△NDF全等,根据全等三角形对应边相等可得ME=NF,根据比例设OM=3k,ON=5k,然后分点M在x轴正半轴和负半轴两种情况,利用ME=NF列式求解即可.
(2)过点B作BE⊥DQ交QD的延长线于E,然后求出△PCQ和△BPE相似,根据相似三角形对应边成比例列式求出PQ的长,再根据m=DQ-PQ计算即可得解;
(3)利用勾股定理列式求出BC、BD、CD,再利用勾股定理逆定理求出∠BDC=90°,过点D作DE⊥x轴于E,作DF⊥y轴于F,根据同角的余角相等求出∠MDE=∠NDF,再利用“角角边”证明△MDE和△NDF全等,根据全等三角形对应边相等可得ME=NF,根据比例设OM=3k,ON=5k,然后分点M在x轴正半轴和负半轴两种情况,利用ME=NF列式求解即可.
解答:解:(1)∵直线y=kx-1过点C,
∴x=0时,y=-1,
∴点C的坐标为(0,-1),
∵抛物线y=ax2-(a+
)x+b经过点C、D(2,-2),
∴
,
解得
,
∴抛物线的解析式为y=
x2-
x-1;
(2)过点B作BE⊥DQ交QD的延长线于E,
∵BP⊥CP,
∴∠CPQ+∠BPE=180°-90°=90°,
∵DQ⊥y轴,
∴∠CPQ+∠PCQ=90°,
∴∠CPQ=∠BPE,
又∵∠PQC=∠E=90°,
∴△PCQ∽△BPE,
∴
=
,
令y=0,则
x2-
x-1=0,
整理得,5x2-13x-6=0,
解得x1=-
,x2=3,
∴点B(3,0),
∴QE=3,
又∵点C(0,-1),D(2,-2),DQ⊥y轴,
∴CQ=2-1=1,BE=2,
∴
=
,
整理得,PQ2-3PQ+2=0,
解得PQ=1或PQ=2(P、D重合,舍去),
∴m=DQ-PQ=2-1=1,
故,当BP⊥CP时,m的值是1;
(3)由勾股定理得,BC=
=
,
BD=
=
,
CD=
=
,
∵BD2+CD2=BC2=10,
∴∠BDC=90°,
由旋转的性质,∠MDN=∠BDC=90°,
过点D作DE⊥x轴于E,作DF⊥y轴于F,
则∠MDE+∠MDF=∠EDF=90°,
∠NDF+∠MDF=∠MDN=90°,
∴∠MDE=∠NDF,
∵点D(2,-2),
∴ME=MF=2,
在△MDE和△NDF中,
,
∴△MDE≌△NDF(AAS),
∴ME=NF,
∵
=
,
∴OM=3k,ON=5k,
①点M在x轴正半轴时,ME=2-3k,NF=5k-2,
∴2-3k=5k-2,
解得k=
,
∴OM=
,ON=
,
点M(
,0),N(0,-
);
②点M在x轴负半轴时,ME=2+3k,NF=5k-2,
∴2+3k=5k-2,
解得k=2,
∴OM=6,ON=10,
点M(-6,0),N(0,-10);
综上所述,M、N的坐标分别为M(
,0),N(0,-
)或M(-6,0),N(0,-10).
∴x=0时,y=-1,
∴点C的坐标为(0,-1),
∵抛物线y=ax2-(a+
| 4 |
| 3 |
∴
|
解得
|
∴抛物线的解析式为y=
| 5 |
| 6 |
| 13 |
| 6 |
(2)过点B作BE⊥DQ交QD的延长线于E,
∵BP⊥CP,
∴∠CPQ+∠BPE=180°-90°=90°,
∵DQ⊥y轴,
∴∠CPQ+∠PCQ=90°,
∴∠CPQ=∠BPE,
又∵∠PQC=∠E=90°,
∴△PCQ∽△BPE,
∴
| CQ |
| PE |
| PQ |
| BE |
令y=0,则
| 5 |
| 6 |
| 13 |
| 6 |
整理得,5x2-13x-6=0,
解得x1=-
| 3 |
| 5 |
∴点B(3,0),
∴QE=3,
又∵点C(0,-1),D(2,-2),DQ⊥y轴,
∴CQ=2-1=1,BE=2,
∴
| 1 |
| 3-PQ |
| PQ |
| 2 |
整理得,PQ2-3PQ+2=0,
解得PQ=1或PQ=2(P、D重合,舍去),
∴m=DQ-PQ=2-1=1,
故,当BP⊥CP时,m的值是1;

(3)由勾股定理得,BC=
| 32+12 |
| 10 |
BD=
| (2-3)2+(-2-0)2 |
| 5 |
CD=
| (2-0)2+(-2+1)2 |
| 5 |
∵BD2+CD2=BC2=10,
∴∠BDC=90°,
由旋转的性质,∠MDN=∠BDC=90°,
过点D作DE⊥x轴于E,作DF⊥y轴于F,
则∠MDE+∠MDF=∠EDF=90°,
∠NDF+∠MDF=∠MDN=90°,
∴∠MDE=∠NDF,
∵点D(2,-2),
∴ME=MF=2,
在△MDE和△NDF中,
|
∴△MDE≌△NDF(AAS),
∴ME=NF,
∵
| OM |
| ON |
| 3 |
| 5 |
∴OM=3k,ON=5k,
①点M在x轴正半轴时,ME=2-3k,NF=5k-2,
∴2-3k=5k-2,
解得k=
| 1 |
| 2 |
∴OM=
| 3 |
| 2 |
| 5 |
| 2 |
点M(
| 3 |
| 2 |
| 5 |
| 2 |
②点M在x轴负半轴时,ME=2+3k,NF=5k-2,
∴2+3k=5k-2,
解得k=2,
∴OM=6,ON=10,
点M(-6,0),N(0,-10);
综上所述,M、N的坐标分别为M(
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,相似三角形的判定与性质,全等三角形的判定与性质,(2)根据BP⊥CP作辅助线构造出相似三角形是解题的关键,(3)作辅助线构造出全等三角形是解题的关键,难点在于要分情况讨论.

练习册系列答案
相关题目
已知点(2,8)在抛物线y=ax2上,则a的值为( )
| A、±2 | ||
B、±2
| ||
| C、2 | ||
| D、-2 |
若(2,0)、(4,0)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是直线( )
| A、x=0 | B、x=1 | C、x=2 | D、x=3 |


 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.