题目内容
已知:关于x的一次函数y=(2m-1)x+m-2若这个函数的图象与y轴负半轴相交,且不经过第二象限,且m为正整数.(1)求这个函数的解析式.
(2)求直线y=-x和(1)中函数的图象与x轴围成的三角形面积.
分析:(1)根据函数图象与负半轴相交可得出m-2<0,再根据图象不经过第二象限可得出2m-1>0,从而结合m为正整数可得出m的值.
(2)求出与x轴和y轴的交点即可得出所围成的三角形的面积.
(2)求出与x轴和y轴的交点即可得出所围成的三角形的面积.
解答:解:(1)由题意得:
,
解得:
<m<2,
又∵m为正整数,
∴m=1,函数解析式为:y=x-1.
(2)由(1)得,函数图象与x轴交点为(1,0)与y轴交点为(0,-1),
∴所围三角形的面积为:
×1×1=
.
|
解得:
| 1 |
| 2 |
又∵m为正整数,
∴m=1,函数解析式为:y=x-1.
(2)由(1)得,函数图象与x轴交点为(1,0)与y轴交点为(0,-1),
∴所围三角形的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查待定系数法求函数解析式及求解三角形面积的知识,难度不大,注意解答此类题目的步骤.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知M、N两点关于y轴对称,且点M在反比例函数 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( )
 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( )A.有最小值,且最小值是 | B.有最大值,且最大值是 |
C.有最大值,且最大值是 | D.有最小值,且最小值是 |
已知M、N两点关于y轴对称,且点M在反比例函数 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数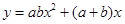 ( )
( )
A.有最小值,且最小值是 | B.有最大值,且最大值是 |
C.有最大值,且最大值是 | D.有最小值,且最小值是 |
 的图象上,点N在一次函 数
的图象上,点N在一次函 数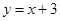 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( ) B.有最大值,且最大值是
B.有最大值,且最大值是 D.有最小值,且最小值是
D.有最小值,且最小值是