题目内容
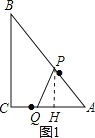
【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm.点P从A出发,沿AB方向,以2cm/s的速度向点B运动,点Q从C出发,沿CA方向,以1cm/s的速度向点A运动;若两点同时出发,当其中一点到达端点时,两点同时停止运动,设运动时间为t(s),△APQ的面积为S(cm2)
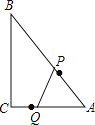
(1)t=2时,则点P到AC的距离是 cm,S= cm2;
(2)t为何值时,PQ⊥AB;
(3)t为何值时,△APQ是以AQ为底边的等腰三角形;
(4)求S与t之间的函数关系式,并求出S的最大值.
【答案】(1)![]() ;
;![]() ;(2)t=
;(2)t=![]() 时,PQ⊥AB;(3)当t=
时,PQ⊥AB;(3)当t=![]() 时,△APQ是以AQ为底边的等腰三角形;(4)t=3时,S最大=
时,△APQ是以AQ为底边的等腰三角形;(4)t=3时,S最大=![]() .
.
【解析】
试题分析:(1)作PH⊥AC于H,根据平行线的性质得到比例式,计算求出点P到AC的距离,根据三角形的面积公式求出△APQ的面积;
(2)根据相似三角形的判定定理证明△APQ∽△ACB,根据相似三角形的性质列出比例式,计算即可;
(3)根据等腰三角形的三线合一和相似三角形的性质解答即可;
(4)根据题意列出二次函数解析式,运用配方法把一般式化为顶点式,根据二次函数的性质解答即可.
解:经过t(s),AP=2t,CQ=t,AQ=6﹣t,
在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm
由勾股定理可求出AB=10cm,
(1)如图1,作PH⊥AC于H,
当t=2时,AP=4cm,AQ=6﹣2=4cm,
∵∠C=90°,PH⊥AC,
∴PH∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得PH=![]() cm,
cm,
S=![]() ×AQ×PH=
×AQ×PH=![]() cm2.
cm2.
故答案为![]() ;
;![]() ;
;
(2)当PQ⊥AB时,又∠C=90°,
∴△APQ∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() .
.
答:t=![]() 时,PQ⊥AB;
时,PQ⊥AB;
(3)如图1,当△APQ是以AQ为底边的等腰三角形时,
AH=![]() AQ,
AQ,
∵△APQ∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得AH=![]() t,
t,
∴![]() t=
t=![]() (6﹣t),
(6﹣t),
解得,t=![]() ,
,
∴当t=![]() 时,△APQ是以AQ为底边的等腰三角形;
时,△APQ是以AQ为底边的等腰三角形;
(4)∵△APQ∽△ACB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,PH=![]() t,
t,
∴S=![]() ×AQ×PH=
×AQ×PH=![]() ×
×![]() t×(6﹣t)=﹣
t×(6﹣t)=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
∴t=3时,S最大=![]() .
.