Question

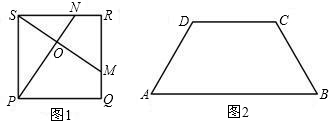
如图①，在正方形ABCD中，E、F、G、H分别为边AB、BC、CD、DA上的点，HA=EB=FC=GD，连接EG、FH，交点为O。

（1）如图②，连接EF、FG、GH、HE，试判断四边形EFGH的形状，并证明你的结论；
（2）将正方形ABCD沿线段EG、HF剪开，再把得到的四个四边形按图③的方式拼接成一个四边形，若正方形ABCD的边长为3cm，HA=EB=FC=GD=1cm，则图③中阴影部分的面积为____cm²。

Answer 1

解：（1）四边形EFGH是正方形。
证明：∵四边形ABCD是正方形，
∴∠A=∠B=∠C=∠D=90°，AB=BC=CD=DA，
∵HA=EB=FC=GD，
∴AE=BF=CG=DH，
∴△AEH≌△BFE≌△CGF≌△DHG，
∴HE=EF=FG=GH，
∴四边形EFGH是菱形，
由△DHG≌△AEH知∠DHG=∠AEH，
∵∠AEH+∠AHE=90°，
∴∠DHG+∠AHE=90°，
∴∠GHE=90°，
∴四边形EFCH是正方形；
（2）1。