题目内容
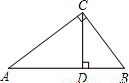
（2001•绍兴）如图，梯形ABCD中，AD∥BC（AD＜BC），AC、BD交于点O，若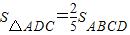
，则△AOD与△BOC的周长比是（ ）
A．1：2
B．2：3
C．3：4
D．4：5
【答案】分析：根据相似三角形的性质及梯形的面积公式，可求得其相似比，再根据相似三角形的周长比等于相似比即可得到答案．
解答：
解：设梯形的高是h，则△ABC的面积是
BC•h
∵梯形ABCD得面积是
（AD+BC）•h，根据
∴BC=
（AD+BC）
∴5AD=2AD+2BC
∴
=
，
∵AD∥BC
∴△AOD∽△COB，
∴△AOD与△BOC的周长比是2：3．
故选B．
点评：本题考查对相似三角形性质的理解，相似三角形周长的比等于相似比．
解答：
解：设梯形的高是h，则△ABC的面积是BC•h∵梯形ABCD得面积是
（AD+BC）•h，根据∴BC=
（AD+BC）∴5AD=2AD+2BC
∴
=，∵AD∥BC
∴△AOD∽△COB，
∴△AOD与△BOC的周长比是2：3．
故选B．
点评：本题考查对相似三角形性质的理解，相似三角形周长的比等于相似比．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
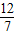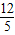cm
cm
cm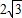
，BD=2，则图中阴影部分的面积是 ．
