题目内容
抛物线y=4x2-4x+3的顶点坐标是( )
| A、(1,2) | ||
| B、(1,-2) | ||
C、(
| ||
D、(-
|
考点:二次函数的性质
专题:
分析:已知抛物线解析式为一般式,利用公式法可求顶点坐标,也可以用配方法求解.
解答:解:利用配方法
y=4x2-4x+3=4(x2-x+
-
)+3=4(x-
)2+2,
故顶点的坐标是(
,2),
故选C.
y=4x2-4x+3=4(x2-x+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
故顶点的坐标是(
| 1 |
| 2 |
故选C.
点评:本题考查了二次函数的性质,求抛物线的顶点坐标、对称轴及最值通常有两种方法:(1)公式法;(2)配方法.

练习册系列答案
相关题目
如果不等式组
的解是x>a,那么a的取值范围是( )
|
| A、a≥4 | B、a≤4 | C、a=4 |
如果a>b,那么下列不等式中不正确的是( )
| A、a-2>b-2 | ||||
B、
| ||||
| C、-2a<-2b | ||||
| D、a+1<b-1 |
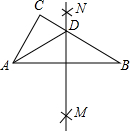 如图,在△ABC中,分别以点A和点B为圆心,大于
如图,在△ABC中,分别以点A和点B为圆心,大于| 1 |
| 2 |
| A、20 | B、17 | C、14 | D、7 |
已知一个等腰三角形的顶角为46°,则它腰上的高与底边所成的角等于( )
| A、23° | B、44° |
| C、46° | D、67° |
下列四个命题中,是真命题的有( )
①锐角都小于直角;②相等的角是对顶角;③内错角相等;④直角都相等.
①锐角都小于直角;②相等的角是对顶角;③内错角相等;④直角都相等.
| A、1个 | B、2个 | C、3个 | D、4个 |