题目内容
如图,直线y= x+
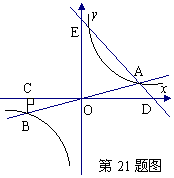
x+ 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )

A.3 B.4 C.5 D.6
【答案】
A
【解析】
试题分析:根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.

∵直线y= x+
x+ 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),
∴A点的坐标为0= x+
x+
x=-3,A(-3,0),
B点的坐标为:(0, ),
),
∴AB=2
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
根据△AP1C1∽△ABO,

∴AP1=2,
∴P1的坐标为:(-1,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
根据△AP2C2∽△ABO,

∴AP2=2,
P2的坐标为:(-5,0),
从-1到-5,整数点有-2,-3,-4,故横坐标为整数的点P的个数是3个.
故选A.
考点:直线与坐标轴的求法,相似三角形的判定
点评:本题综合性较强,难度较大,在中考中比较常见,注意特殊点的求法是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 x+
x+ 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
