题目内容
如图,已知矩形 ,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.(1)求△PEF的边长;
(2)在不添加辅助线的情况下,当F与C不重合时,先直接判断△APH与△CFH是如下关系中的哪一种:然后证明你的判断.
①△APH与△CFH全等;
②△APH与△CFH相似;
③△APH与△CFH成中心对称;
④△APH与△CFH成轴对称;
(3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论.

【答案】分析:(1)△PEF的高等于矩形的长,过P作PQ⊥BC于Q,利用三角函数即可求解;
(2)根据AD∥BC即可证明两个三角形相似;
(3)根据等角对等边即可证明FC=FH,根据PH+FH=2,BE+EF+FC=3即可求解.
解答: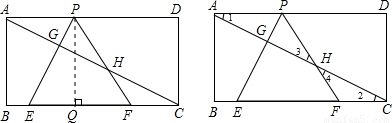 解:(1)过P作PQ⊥BC于Q
解:(1)过P作PQ⊥BC于Q
∵矩形ABCD∴∠B=90°,即AB⊥BC,又AD∥BC∴
∵△PEF是等边三角形∴∠PFQ=60°在Rt△PQF中, ∴PF=2∴△PEF的边长为2. (4分)
∴PF=2∴△PEF的边长为2. (4分)
(2)判断:△APH∽△CFH∵矩形ABCD∴AD∥BC∴∠2=∠1
又∵∠3=∠4,∴△APH∽△CFH (9分)
(3)猜想:PH与BE的数量关系是:PH-BE=1
证法一:在Rt△ABC中, ∴
∴
∴∠1=30°,∵△PEF是等边三角形,∴∠2=60°,PF=EF=2,∵∠2=∠1+∠3,∴∠3=30°
∴∠1=∠3,∴FC=FH,∵PH+FH=2,BE+EF+FC=3,∴PH-BE=1

证法二:在Rt△ABC中, ,∴
,∴
∴∠1=30°∵△PEF是等边三角形,PE=2,∴∠2=∠4=∠5=60°,∴∠6=90°
在Rt△CEG中,∠1=30°,∴ ,即
,即
在Rt△PGH中,∠7=30°,∴ ,∴
,∴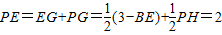 ,∴PH-BE=1
,∴PH-BE=1
证法三:在Rt△ABC中, ,∴
,∴ ,
,
AC2=AB2+BC2,∴ ,∵△PEF是等边三角形,∴∠4=∠5=60°
,∵△PEF是等边三角形,∴∠4=∠5=60°
∴∠6=∠8=90°,∴△EGC∽△PGH,∴ ,∴
,∴
①∵∠1=∠1,∠B=∠6=90°,∴△CEG∽△CAB,∴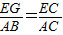 ,即
,即 ,∴
,∴
②把②代入①得, ,∴PH-BE=1 (14分)
,∴PH-BE=1 (14分)
点评:本题主要考查了等边三角形的计算,以及相似三角形的判定与性质,等腰三角形的计算可以通过作高线转化为直角三角形的计算.
(2)根据AD∥BC即可证明两个三角形相似;
(3)根据等角对等边即可证明FC=FH,根据PH+FH=2,BE+EF+FC=3即可求解.
解答:
 解:(1)过P作PQ⊥BC于Q
解:(1)过P作PQ⊥BC于Q∵矩形ABCD∴∠B=90°,即AB⊥BC,又AD∥BC∴

∵△PEF是等边三角形∴∠PFQ=60°在Rt△PQF中,
 ∴PF=2∴△PEF的边长为2. (4分)
∴PF=2∴△PEF的边长为2. (4分)(2)判断:△APH∽△CFH∵矩形ABCD∴AD∥BC∴∠2=∠1
又∵∠3=∠4,∴△APH∽△CFH (9分)
(3)猜想:PH与BE的数量关系是:PH-BE=1
证法一:在Rt△ABC中,
 ∴
∴
∴∠1=30°,∵△PEF是等边三角形,∴∠2=60°,PF=EF=2,∵∠2=∠1+∠3,∴∠3=30°
∴∠1=∠3,∴FC=FH,∵PH+FH=2,BE+EF+FC=3,∴PH-BE=1

证法二:在Rt△ABC中,
 ,∴
,∴
∴∠1=30°∵△PEF是等边三角形,PE=2,∴∠2=∠4=∠5=60°,∴∠6=90°
在Rt△CEG中,∠1=30°,∴
 ,即
,即
在Rt△PGH中,∠7=30°,∴
 ,∴
,∴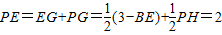 ,∴PH-BE=1
,∴PH-BE=1证法三:在Rt△ABC中,
 ,∴
,∴ ,
,AC2=AB2+BC2,∴
 ,∵△PEF是等边三角形,∴∠4=∠5=60°
,∵△PEF是等边三角形,∴∠4=∠5=60°∴∠6=∠8=90°,∴△EGC∽△PGH,∴
 ,∴
,∴
①∵∠1=∠1,∠B=∠6=90°,∴△CEG∽△CAB,∴
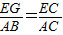 ,即
,即 ,∴
,∴
②把②代入①得,
 ,∴PH-BE=1 (14分)
,∴PH-BE=1 (14分)点评:本题主要考查了等边三角形的计算,以及相似三角形的判定与性质,等腰三角形的计算可以通过作高线转化为直角三角形的计算.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.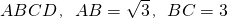 ,在BC上取两点E,F(E在F左边),
,在BC上取两点E,F(E在F左边), 以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.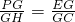 ;
; 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
 ,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.