��Ŀ����
�������߶γ�Ϊ2��4Ϊ�߹����ı�������4�֣�
��1���ٵ���A=60��ʱ��ֱ��д������1��3���ı���ABCD�������
��������2�У���A�ܷ����60�㣿˵�����ɣ�
��������4�У�����A=60��ʱ�����ı���ABCD�������
��2������4������������У��ֱ�д������4�����ݵļ���
����4�������У��ֱ�д�������ĸ����ݵķ��
��3����2�����ݣ�����a a a 3����a 3 3 3����Ƚ���2�����ݵķ���Ĵ�С��
| ����1 | ����2 | ����3 | ����4 | |
| ���� | AB=4��BC=2��CD=4��DA=2 | AB=4��BC=2��CD=2��DA=4 | AB=4��BC=2��CD=2��DA=2 | AB=4��BC=4��CD=2��DA=4 |
| ͼ�� | 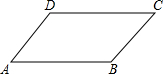 |
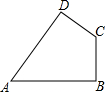 |
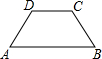 |
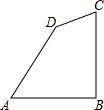 |
��������2�У���A�ܷ����60�㣿˵�����ɣ�
��������4�У�����A=60��ʱ�����ı���ABCD�������
��2������4������������У��ֱ�д������4�����ݵļ���
����4�������У��ֱ�д�������ĸ����ݵķ��
��3����2�����ݣ�����a a a 3����a 3 3 3����Ƚ���2�����ݵķ���Ĵ�С��
��������1���ٹ�D��DE��AB��E�������ADE=30�㣬�����DE������ƽ���ı��ε������ʽ������ɣ�����ı����ǵ������Σ�������εĸߣ����������ʽ������ɣ�
������BD���ó��ȱ�������ABD�����BD=CD+BC���������������߹�ϵ�����жϼ��ɣ�
������BD����B��BH��DC��H����D��DE��AB��E���ֱ������ABD�͡�BDC���������������𰸣�
��2���ٸ��ݼ����������ɣ�
����������ݵ�ƽ�������ٸ��ݷ��ʽ������ɣ�
��3����������ݵ�ƽ�������ٸ��ݷ��ʽ������ɣ�
������BD���ó��ȱ�������ABD�����BD=CD+BC���������������߹�ϵ�����жϼ��ɣ�
������BD����B��BH��DC��H����D��DE��AB��E���ֱ������ABD�͡�BDC���������������𰸣�
��2���ٸ��ݼ����������ɣ�
����������ݵ�ƽ�������ٸ��ݷ��ʽ������ɣ�
��3����������ݵ�ƽ�������ٸ��ݷ��ʽ������ɣ�
����⣺��1����
��D��DE��AB��E��
���DEA=90�㣬
�ߡ�A=60�㣬
���ADE=30�㣬
��AD=2��
��AE=
AD=1��
���ɹ��ɶ����ã�DE=
��
��AD=BC=2��AB=DC=4��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�������AB��DE=4
��

��ͼ��

��AB��ȡһ��F��ʹAD=DF=2����D����D��DE��AB��E��
��DE=
��
��AD=DF����A=60��
���ADF�ǵȱ������Σ�
��AF=AD=2��DF=AD=BC=2��
��AB=4��
��BF=4-2=2=DC��
���ı���DFBC��ƽ���ı��Σ�
��DC��AB��
���ı���ADCB�ǵ������Σ�
���ı���ABCD�������
��DC+AB����DE=
����2+4����
=3
��
��
������2�У���A���ܵ���60�㣬
�����ǣ���ͼ������BD��
��AB=4��DA=4������A=60��ʱ����ABD�ǵȱ������Σ�
��BD=AB=4=2+2=DC+BC�����������������߹�ϵ������
��������2�У���A���ܵ���60�㣮
��
��ͼ������BD����B��BH��DC��H����D��DE��AB��E��
���AED=90�㣬
�ߡ�A=60�㣬AB=AD=4��
���ADE=30�㣬
��DE=AD•cos60��=2
��
��AB=AD=4����A=60�㣬
���ABD�ǵȱ������Σ�
��BD=4=BC��
��BH��DC��
��CH=DH=
DC=
��2=1��
�ڡ�BHD�У��й��ɶ����ã�BH=
=
��
���ı���ABCD�����S=S��ADB+S��BDC=
��4��2
+
��2��
=4
+
��
��2����4�����ݵļ����4-2=4��
�ڡ�����1��������4��4��2��2��
��ƽ������
����4+4+2+2��=3��
�ࣨ4-3��2+��4-3��2+��2-3��2+��2-3��2=4��
������S12=
��4=1��
ͬ��������2�ķ�����1��
����3��������������4��2��2��2��
��ƽ������
����4+2+2+2��=2.5��
�ࣨ4-2.5��2+��2-2.5��2+��2-2.5��2+��2-2.5��2=3��
������S32=
��3=0.75��
����4����������4��4����4��2��
��ƽ������
����4+4+4+2��=3.5��
�ࣨ4-3.5��2+��4-3.5��2+��4-3.5��2+��2-3.5��2=3��
������S42=
��3=0.75��
��4�����ݵķ�������Ϊ1��1��0.75��0.75��
��3����I����a a a 3��
��ƽ������
��a+a+a+3��=
��
�ࣨa-
��2+��a-
��2+��a-
��2+��3-
��2=
��
������=
��
=3����
��2��
����a 3 3 3��
��ƽ������
��a+3+3+3��=
��
�ࣨa-
��2+��3-
��2+��3-
��2+��3-
��2=
��
������=
��
=3����
��2��
��2�����ݵķ�����ȣ�

��D��DE��AB��E��
���DEA=90�㣬
�ߡ�A=60�㣬
���ADE=30�㣬
��AD=2��
��AE=
| 1 |
| 2 |
���ɹ��ɶ����ã�DE=
| 3 |
��AD=BC=2��AB=DC=4��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�������AB��DE=4
| 3 |

��ͼ��

��AB��ȡһ��F��ʹAD=DF=2����D����D��DE��AB��E��
��DE=
| 3 |
��AD=DF����A=60��
���ADF�ǵȱ������Σ�
��AF=AD=2��DF=AD=BC=2��
��AB=4��
��BF=4-2=2=DC��
���ı���DFBC��ƽ���ı��Σ�
��DC��AB��
���ı���ADCB�ǵ������Σ�
���ı���ABCD�������
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
��

������2�У���A���ܵ���60�㣬
�����ǣ���ͼ������BD��
��AB=4��DA=4������A=60��ʱ����ABD�ǵȱ������Σ�
��BD=AB=4=2+2=DC+BC�����������������߹�ϵ������
��������2�У���A���ܵ���60�㣮
��

��ͼ������BD����B��BH��DC��H����D��DE��AB��E��
���AED=90�㣬
�ߡ�A=60�㣬AB=AD=4��
���ADE=30�㣬
��DE=AD•cos60��=2
| 3 |
��AB=AD=4����A=60�㣬
���ABD�ǵȱ������Σ�
��BD=4=BC��
��BH��DC��
��CH=DH=
| 1 |
| 2 |
| 1 |
| 2 |
�ڡ�BHD�У��й��ɶ����ã�BH=
| 42-12 |
| 15 |
���ı���ABCD�����S=S��ADB+S��BDC=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 15 |
| 3 |
| 15 |
��2����4�����ݵļ����4-2=4��
�ڡ�����1��������4��4��2��2��
��ƽ������
| 1 |
| 4 |
�ࣨ4-3��2+��4-3��2+��2-3��2+��2-3��2=4��
������S12=
| 1 |
| 4 |
ͬ��������2�ķ�����1��
����3��������������4��2��2��2��
��ƽ������
| 1 |
| 4 |
�ࣨ4-2.5��2+��2-2.5��2+��2-2.5��2+��2-2.5��2=3��
������S32=
| 1 |
| 4 |
����4����������4��4����4��2��
��ƽ������
| 1 |
| 4 |
�ࣨ4-3.5��2+��4-3.5��2+��4-3.5��2+��2-3.5��2=3��
������S42=
| 1 |
| 4 |
��4�����ݵķ�������Ϊ1��1��0.75��0.75��
��3����I����a a a 3��
��ƽ������
| 1 |
| 4 |
| 3a+3 |
| 4 |
�ࣨa-
| 3a+3 |
| 4 |
| 3a+3 |
| 4 |
| 3a+3 |
| 4 |
| 3a+3 |
| 4 |
| 3(a-3)2 |
| 4 |
������=
| 1 |
| 4 |
| 3(a-3)2 |
| 4 |
| a-3 |
| 4 |
����a 3 3 3��
��ƽ������
| 1 |
| 4 |
| a+9 |
| 4 |
�ࣨa-
| a+9 |
| 4 |
| a+9 |
| 4 |
| a+9 |
| 4 |
| a+9 |
| 3 |
| 3(a-3)2 |
| 4 |
������=
| 1 |
| 4 |
| 3(a-3)2 |
| 4 |
| a-3 |
| 4 |
��2�����ݵķ�����ȣ�
���������⿼���˷������������ε����ʺ��ж���ƽ���ı��ε����ʺ��ж����ȱ������ε����ʺ��ж�����ֱ�������Σ����ɶ�����֪ʶ����ۺ����ã���Ҫ����ѧ�����ö������������ͼ����������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ