Question

【题目】如图，已知直线与抛物线相交于，两点．

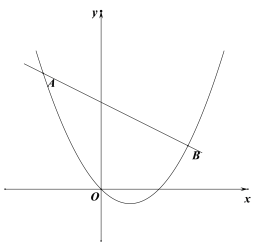
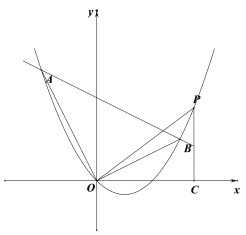
（1）求抛物线的解析式．

（2）在直线下方的抛物线上求点，求的面积等于20．

（3）若在抛物线上，作轴于点，若和相似，求点的坐标．

Answer 1

【答案】（1）；（2）（－2，3）或（4，0）；（3）或或或

【解析】

(1)根据抛物线相交于，两点，用待定系数法列方程组求解即可得到答案；

(2)作PD//y轴，交AB于点D，设，则，把BD的长度表示出来，再根据三角形的面积公式列等式，求解即可得到答案；

(3)先用勾股定理的逆定理证明∠AOB=，再分CPO∽OBA 或者CPO∽OBA两种情况讨论即可得到答案；

解：（1）∵抛物线相交于，两点，

将A（－4，8），B(6，3)代入，联立得：

，

解得，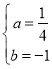

所求的抛物线的解析式为：．

（2）如图，作PD//y轴，交AB于点D，

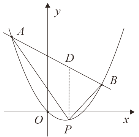
设，则，

∴ ，

，

∴，

解得：，，

当时，，

当时，，

故所求的点P为（－2，3）或（4，0）．

（3）设，如图，

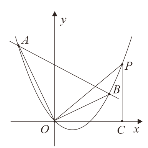
根据勾股定理得到：，

，，

∴，

∴∠AOB=（勾股定理的逆定理），

∠AOB=∠PCO，

当时，CPO∽OBA ．

即：，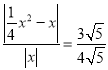

整理得：，

解方程：，得（舍去），，此时P点坐标为；

解方程：，得（舍去），，此时P点坐标为．

当时，CPO∽OBA ．

解即：，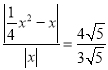

整理得：，

解方程：，得（舍去），，此时P点坐标为．

解方程：，得（舍去），，此时P点坐标．

综上所述，所求点P的坐标为：或或或．