题目内容
在△ABC中，点D、E分别在直线AB、AC上，DE∥BC，AB=1，AC=2，AD=3，那么CE=________．
4或8
分析：可依据题意作出简单的图形，进而结合图形进行分析．题中点D、E分别在直线AB、AC上，由AD的长度则其可能在AB、AC的延长线上，也可能在其反向延长线上，故有两种可能，应分开来求解．
解答：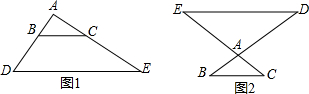
解：如图，
如图1，∵AB=1，AC=2，AD=3，且DE∥BC，
∴AB：AD=AC：AE，解得AE=6，即CE=4；
同理图2中则CE=AC+AE=2+6=8．
故答案为4或8．
点评：本题主要考查了相似三角形的判定及性质问题，能够熟练掌握．
分析：可依据题意作出简单的图形，进而结合图形进行分析．题中点D、E分别在直线AB、AC上，由AD的长度则其可能在AB、AC的延长线上，也可能在其反向延长线上，故有两种可能，应分开来求解．
解答：
解：如图，如图1，∵AB=1，AC=2，AD=3，且DE∥BC，
∴AB：AD=AC：AE，解得AE=6，即CE=4；
同理图2中则CE=AC+AE=2+6=8．
故答案为4或8．
点评：本题主要考查了相似三角形的判定及性质问题，能够熟练掌握．
练习册系列答案
相关题目
∠ACB的外角平分线于点F．
如图，在△ABC中，点D，E分别在边AB，AC上，给出5个论断：①CD⊥AB；②BE⊥AC；③AE=CE；④∠ABE=30°；⑤CD=BE．
（2013•上海）如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB=3：5，那么CF：CB等于（ ）