题目内容
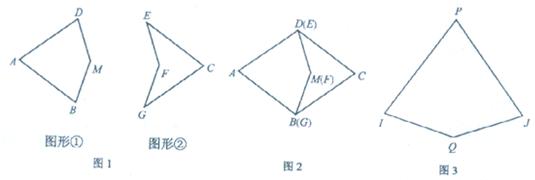
如图，记边长为a的正方形ABCD的面积为P，边长为b的正方形AEFG的面积为Q，长为a宽为b的长方形ABHG．AELD的面积为R，边长为a-b的小正方形FHCL的面积为S．
（1）请你用P、Q、R表示S，S=______；
（2）将（1）所得到的结论，用含a、b的代数式表示，则有（a-b）2=______；
（3）请你利用你发现的结论进行简便运算：20102-2×2010×1949+19492．
解：（1）由图可知，S=P-Q-2（R-Q）=P-2R+Q；
（2）（a-b）2=a2-2ab+b2；
（3）20102-2×2010×1949+19492
=（2010-1949）2
=612
=3721．
故答案为：（1）P-2R+Q；（2）a2-2ab+b2．
分析：（1）根据S等于大正方形的面积减去小正方形AEFG的面积再减去两个小长方形的面积列式整理即可得解；
（2）把相应的面积换成a、b表示的代数式即可；
（3）利用（2）的公式计算即可得解．
点评：本题考查了列代数式，主要是完全平方公式的几何背景的考查，仔细观察图形是解题的关键．
（2）（a-b）2=a2-2ab+b2；
（3）20102-2×2010×1949+19492
=（2010-1949）2
=612
=3721．
故答案为：（1）P-2R+Q；（2）a2-2ab+b2．
分析：（1）根据S等于大正方形的面积减去小正方形AEFG的面积再减去两个小长方形的面积列式整理即可得解；
（2）把相应的面积换成a、b表示的代数式即可；
（3）利用（2）的公式计算即可得解．
点评：本题考查了列代数式，主要是完全平方公式的几何背景的考查，仔细观察图形是解题的关键．
练习册系列答案
相关题目
