题目内容
(本题满分9分)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D.飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.

见解析
解析:在Rt△ABD中,∵∠BAD=30°
∴BD=AB·tan30°=6×=2 ………………………………………………2分
∵∠BAC=60°∴∠ABC=30°∴∠ACB=90°
∴BC=AB·cos30°=6×=3 ………………………………………………4分
过点C作CE⊥BD于E,则∠CBE=60°,CE=BC·sin60°=………………6分
∴BE=BC·cos60°=…………………………………………………………7分
DE=BD-BE=2-=
∴在Rt△CDE中,CD===(km)
答:山头C、D之间的距离为 km …………………………………………9分

练习册系列答案
相关题目
.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?


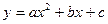 交
交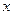 轴于
轴于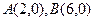 两点,交
两点,交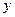 轴于点
轴于点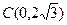 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交