题目内容
若|x+y-1|+
=0,则yx=( )
| 2x+y+1 |
| A、-6 | ||
B、
| ||
| C、-9 | ||
D、
|
分析:因为绝对值一定都是大于等于零的,故|x+y-1|≥0,又由算术平方根的性质知2x+y+1≥0,要使等式成立,则必须满足x+y-1=0,2x+y+1=0.
解答:解:由x+y-1=0,2x+y+1=0,
解得 x=-2 y=3
则 yx=3-2=
故选D.
解得 x=-2 y=3
则 yx=3-2=
| 1 |
| 9 |
故选D.
点评:掌握绝对值和算术平方根的性质.

练习册系列答案
相关题目
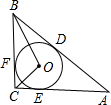 如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=
如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=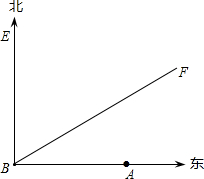 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.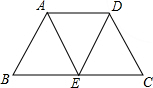 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗?
在等腰梯形ABCD中,AD∥BC,E是BC的中点,连接AE,DE,AE与DE相等吗? 13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=
13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=