题目内容
(2011•金华)在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C.
(1)当n=1时,如果a=﹣1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O.
①试求当n=3时a的值;
②直接写出a关于n的关系式.
(1)解:由题意可知,抛物线对称轴为直线x=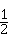 ,
,
∴ ,得b=1,
,得b=1,
答:b的值是1.
(2)解:设所求抛物线解析式为y=ax2+bx+1,
由对称性可知抛物线经过点B(2,1)和点M(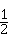 ,2),
,2), ,
,
解得
∴所求抛物线解析式为 ,
,
答:此时抛物线的解析式是 .
.
(3)解:①当n=3时,OC=1,BC=3,
设所求抛物线解析式为y=ax2+bx,
过C作CD⊥OB于点D,则Rt△OCD∽Rt△CBD,
∴ ,
,
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+t2=12,∴ ,
,
∴C( ,
, ),又B(
),又B( ,0),
,0),
∴把B、C坐标代入抛物线解析式,得
解得:a= ,
,
答:a的值是﹣ .
.
②答:a关于n的关系式是 .
.
解析

练习册系列答案
相关题目
(2011•金华)在中国旅游日(5月19日),我市旅游部门对2011年第一季度游客在金华的旅游时间作抽样调查,统计如下:
若将统计情况制成扇形统计图,则表示旅游时间为“2~3天”的扇形圆心角的度数为_____
| 旅游时间 | 当天往返 | 2~3天 | 4~7天 | 8~14天 | 半月以上 | 合计 |
| 人数(人) | 76 | 120 | 80 | 19 | 5 | 300 |
(2011?金华)在中国旅游日(5月19日),我市旅游部门对2011年第一季度游客在金华的旅游时间作抽样调查,统计如下:
| 旅游时间 | 当天往返 | 2~3天 | 4~7天 | 8~14天 | 半月以上 | 合计 |
| 人数(人) | 76 | 120 | 80 | 19 | 5 | 300 |

