题目内容
如图，四边形ABCD是正方形，△PAD是等边三角形，则∠BPC等于
- A.20°
- B.30°
- C.35°
- D.40°
B
分析：正方形的四个角相等，四个边相等，等边三角形三个角相等，三个边相等，从而求出∠ABP，进而求出∠PBC的度数，从而得到∠BPC的度数．
解答：∵四边形ABCD是正方形，△PAD是等边三角形，
∴∠BAP=∠BAD+∠PAB=90°+60°=150°．
∵PA=AD，AB=AD，
∴PA=AB，
∴∠ABP=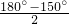
=15°，
∴∠PBC=∠ABC-∠ABP=90°-15°=75°，
同理：∠PCB=75°，
∴∠BPC=180°-75°-75°=30°．
故选B．
点评：本题考查了正方形的性质和等边三角形的性质，和三角形的内角和为180°．
分析：正方形的四个角相等，四个边相等，等边三角形三个角相等，三个边相等，从而求出∠ABP，进而求出∠PBC的度数，从而得到∠BPC的度数．
解答：∵四边形ABCD是正方形，△PAD是等边三角形，
∴∠BAP=∠BAD+∠PAB=90°+60°=150°．
∵PA=AD，AB=AD，
∴PA=AB，
∴∠ABP=
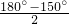=15°，∴∠PBC=∠ABC-∠ABP=90°-15°=75°，
同理：∠PCB=75°，
∴∠BPC=180°-75°-75°=30°．
故选B．
点评：本题考查了正方形的性质和等边三角形的性质，和三角形的内角和为180°．
练习册系列答案
相关题目
如图，四边形ABCD的对角线AC与BD互相垂直平分于点O，设AC=2a，BD=2b，请推导这个四边形的性质．（至少3条）
如图，四边形ABCD的对角线AC、BD交于点P，过点P作直线交AD于点E，交BC于点F．若PE=PF，且AP+AE=CP+CF．
如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数．
如图，四边形ABCD为正方形，E是BC的延长线上的一点，且AC=CE，求∠DAE的度数．