Question

【题目】在综合与实践课上，老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.

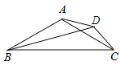
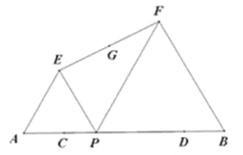
（1）奋进小组用图1中的矩形纸片ABCD，按照如图2所示的方式，将矩形纸片沿对角线AC折叠，使点B落在点处，则与重合部分的三角形的类型是________.

（2）勤学小组将图2中的纸片展平，再次折叠，如图3，使点A与点C重合，折痕为EF，然后展平，则以点A、F、C、E为顶点的四边形是什么特殊四边形？请说明理由．

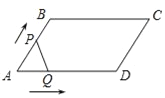
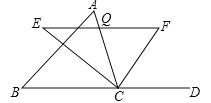
（3）创新小组用图4中的矩形纸片ABCD进行操作，其中，，先沿对角线BD对折，点C落在点的位置，交AD于点G，再按照如图5所示的方式折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M．则EM的长为________cm.

Answer 1

【答案】（1）等腰三角形（或钝角三角形）；（2）菱形，理由详见解析；（3）.

【解析】

（1）利用折叠的性质和角平分线定义即可得出结论；
（2）利用四边相等的四边形是菱形即可得出结论；
（3）由勾股定理可求BD的长，BG的长，AG的长，利用勾股定理和折叠的性质可得到结果。

解：（1）等腰三角形（或钝角三角形）．

提示：∵四边形ABCD是矩形，

∴，

∴．

由折叠知，，

∴，

∴重合部分的三角形是等腰三角形.

（2）菱形．

理由：如图，

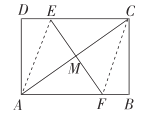
连接AE、CF，设EF与AC的交点为M，

由折叠知，，，

∴，．

∵四边形ABCD是矩形，

∴，

∴，，

∴，

∴，

∴，

∴以点A，F，C，E为顶点的四边形是菱形．

（3）.

提示：∵点D与点A重合，得折痕EN，，，

∴.

在中，，

∴.

∵，，

∴．

∵，

∴，

∴，

∴由勾股定理可得，

由折叠的性质可知，

∵，

∴，

∴，

∴，设，则．

由勾股定理得，即，

解得，即.