题目内容
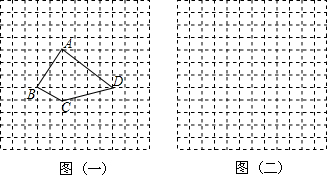
 如图.方格纸中每个小方格都是边长为1个单位的小正方形.请在所给方格纸中.以格点A为顶点分别画格点三角形ABC与格点三角形ADE,使其满足下列条件:
如图.方格纸中每个小方格都是边长为1个单位的小正方形.请在所给方格纸中.以格点A为顶点分别画格点三角形ABC与格点三角形ADE,使其满足下列条件:(1)△ABC为钝角三角形且S△ABC=2;
(2)△ADE∽△ABC且S△ADE:S△ABC=2:1,并说明理由.
分析:(1)根据三角形面积公式假设底边长为2,求出高即可得出答案;
(2)根据△ADE∽△ABC且S△ADE:S△ABC=2:1,即可得出三角形的边长比为
:1,进而求出△ADE的边长即可.
(2)根据△ADE∽△ABC且S△ADE:S△ABC=2:1,即可得出三角形的边长比为
| 2 |
解答: 解:(1)假设AB=2,即可得出△ABC的高为2,画出图形即可;
解:(1)假设AB=2,即可得出△ABC的高为2,画出图形即可;
(2)∵△ADE∽△ABC且S△ADE:S△ABC=2:1,
∴可得出三角形的边长比为
:1,根据△ABC的边长为:
2,2
,2
,
∴△ADE的三边长分别为:2
,4,2
.
 解:(1)假设AB=2,即可得出△ABC的高为2,画出图形即可;
解:(1)假设AB=2,即可得出△ABC的高为2,画出图形即可;(2)∵△ADE∽△ABC且S△ADE:S△ABC=2:1,
∴可得出三角形的边长比为
| 2 |
2,2
| 2 |
| 5 |
∴△ADE的三边长分别为:2
| 2 |
| 10 |
点评:此题主要考查了图形的相似变换,根据已知得出三角形三边关系是解决问题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
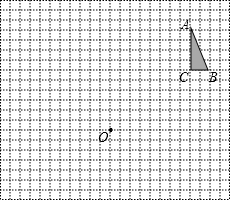 如图,方格纸中每个小正方形的边长都是单位1.
如图,方格纸中每个小正方形的边长都是单位1.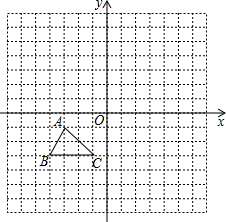 系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).
系后,△ABC的顶点在格点上,点B的坐标为(-4.-3).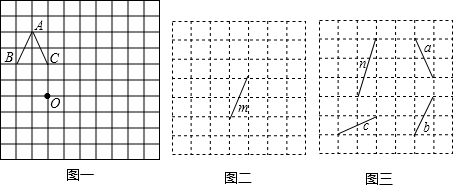
 如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC和点S的位置如图所示.