题目内容
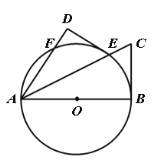
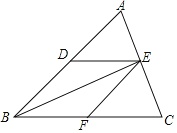
【题目】如图，在
中，D、E、F分别是AB、AC、BC的中点，
（1）求证：四边形DEFB是平行四边形；
（2）如果四边形DEFB是菱形，判断BE与AC的位置关系，并证明.
【答案】（1）证明见解析；（2）BE⊥AC，证明见解析.
【解析】
（1）由三角形中位线定理得到DE∥BC，且DE=
BC，然后根据BF=BC可得证；
（2）由菱形的性质可求出BA=BC，再根据E是AC的中点可得答案.
解：（1）∵D、E、F分别是AB、AC、BC的中点，
∴DE∥BC，且DE=BC，
∵BF=BC，
∴DE=BF，
∴四边形DEFB是平行四边形；
（2）BE⊥AC，
证明：∵四边形DEFB是菱形，
∴BD=BF，
∴BA=BC，
∵E是AC的中点，
∴BE⊥AC.
练习册系列答案
相关题目
