题目内容
 如图所示,在⊙O中,
如图所示,在⊙O中,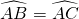 ,∠A=30°,则∠B=
,∠A=30°,则∠B=
- A.150°
- B.75°
- C.60°
- D.15°
B
分析:先根据等弧所对的弦相等求得AB=AC,从而判定△ABC是等腰三角形;然后根据等腰三角形的两个底角相等得出∠B=∠C;最后由三角形的内角和定理求角B的度数即可.
解答:∵在⊙O中,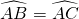 ,
,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B=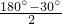 =75°(三角形内角和定理).
=75°(三角形内角和定理).
故选B.
点评:本题综合考查了圆心角、弧、弦的关系,以及等腰三角形的性质.解题的关键是根据等弧对等弦推知△ABC是等腰三角形.
分析:先根据等弧所对的弦相等求得AB=AC,从而判定△ABC是等腰三角形;然后根据等腰三角形的两个底角相等得出∠B=∠C;最后由三角形的内角和定理求角B的度数即可.
解答:∵在⊙O中,
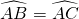 ,
,∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B=
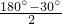 =75°(三角形内角和定理).
=75°(三角形内角和定理).故选B.
点评:本题综合考查了圆心角、弧、弦的关系,以及等腰三角形的性质.解题的关键是根据等弧对等弦推知△ABC是等腰三角形.

练习册系列答案
相关题目
 如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN=
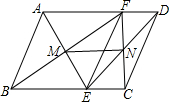
如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN= 如图所示,在△ABC中,∠C=90°,D是AC边上一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.
如图所示,在△ABC中,∠C=90°,D是AC边上一点,且AD=DB=5,CD=3,求tan∠CBD和sinA.

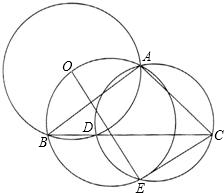 如图所示,在△ABC中,已知D是BC边上的点,O为△ABD的外接圆圆心,△ACD的外接圆与△AOB的外接圆相交于A,E两点.求证:OE⊥EC.
如图所示,在△ABC中,已知D是BC边上的点,O为△ABD的外接圆圆心,△ACD的外接圆与△AOB的外接圆相交于A,E两点.求证:OE⊥EC.