题目内容
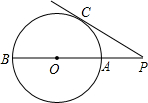如图，PC是⊙O的切线，切点为C，割线PAB过圆心O，交⊙O于点A、B，PC=2，PA=1，则PB的长为
- A.5
- B.4
- C.3
- D.2
B
分析：连接AC，BC，由PC为圆O的切线，根据弦切角等于夹弧所对的圆周角得到一对角相等，再由一对公共角相等，利用两对对应角相等的两三角形相似得到三角形ACP与三角形CBP相似，根据相似得比例列出关系式，将PC及PA的值代入即可求出PB的长．
解答：连接AC，BC，如图所示：
∵PC为圆O的切线，
∴∠ACP=∠B，又∠P=∠P，
∴△ACP∽△CBP，
∴
=
，
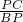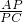又∵PC=2，PA=1，
∴BP=
=4．
故选B
点评：此题考查了切线的性质，相似三角形的判定与性质，以及弦切角的性质，熟练掌握切线的性质是解本题的关键．
分析：连接AC，BC，由PC为圆O的切线，根据弦切角等于夹弧所对的圆周角得到一对角相等，再由一对公共角相等，利用两对对应角相等的两三角形相似得到三角形ACP与三角形CBP相似，根据相似得比例列出关系式，将PC及PA的值代入即可求出PB的长．
解答：连接AC，BC，如图所示：
∵PC为圆O的切线，
∴∠ACP=∠B，又∠P=∠P，
∴△ACP∽△CBP，
∴
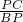=，又∵PC=2，PA=1，
∴BP=
=4．故选B
点评：此题考查了切线的性质，相似三角形的判定与性质，以及弦切角的性质，熟练掌握切线的性质是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
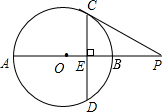如图，AB是⊙O的直径，P为AB延长线上一点，PC切⊙O于点C，过点C作CD⊥AB，垂足为E，并交⊙O于D．
如图，AB是⊙O的直径，P是AB的延长线上的一点，PC切⊙O于点C，⊙O的半径为3，∠PCB=30度．
如图，P是⊙O的直径BC延长线上一点，PA切⊙O于点A，若PC=2，BC=6，则切线PA的长为（ ）| A、无限长 | ||
B、
| ||
| C、4 | ||
D、
|
如图，PA是⊙O的割线，且经过圆心O，与⊙O交于B、A两点，PD切⊙O于点D，AC是⊙O的一条弦，连结PC，且PC=PD．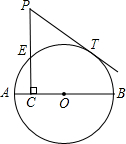
如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．