题目内容
 如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.
如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.(1)求证:PC是⊙O的切线;
(2)若AC=PD,连结BC.求证:AB=2BC.
分析:(1)如图,连接OC、OD.同全等三角形的判定定理证得SSS推知Rt△OCP≌Rt△ODP,则∠OCP=∠ODP=90°,即OC⊥PC,所以PC是⊙O的切线;
(2)通过全等三角形(△AOC≌△PBC)的对应边相等知BC=OC,所以易证AB=2BC.
(2)通过全等三角形(△AOC≌△PBC)的对应边相等知BC=OC,所以易证AB=2BC.
解答: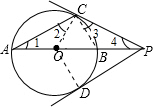 (1)证明:如图,连接OC、OD.
(1)证明:如图,连接OC、OD.
∵PD切⊙O于点D,
∴∠ODP=90°.
∵在△OCP与△ODP中,
,
∴△OCP≌△ODP,
∴∠OCP=∠ODP=90°,即OC⊥PC,
又OC是半径,
∴PC是⊙O的切线;
(2)如图,连接BC.
∵PC、PD是⊙O的两条切线,
∴PC=PD.
又∵AC=PD,
∴AC=PC.
∴∠1=∠4.
∵AB是直径,
∴∠ACB=90°.
又由(1)知,∠OCP=90°,
∴∠2=∠3,
∴在△AOC与△PBC中,
,
∴△AOC≌△PBC(ASA),
∴BC=OC,
∴OA=OB=BC
∴AB=OA+OB=2BC.
 (1)证明:如图,连接OC、OD.
(1)证明:如图,连接OC、OD.∵PD切⊙O于点D,
∴∠ODP=90°.
∵在△OCP与△ODP中,
|
∴△OCP≌△ODP,
∴∠OCP=∠ODP=90°,即OC⊥PC,
又OC是半径,
∴PC是⊙O的切线;
(2)如图,连接BC.
∵PC、PD是⊙O的两条切线,
∴PC=PD.
又∵AC=PD,
∴AC=PC.
∴∠1=∠4.
∵AB是直径,
∴∠ACB=90°.
又由(1)知,∠OCP=90°,
∴∠2=∠3,
∴在△AOC与△PBC中,
|
∴△AOC≌△PBC(ASA),
∴BC=OC,
∴OA=OB=BC
∴AB=OA+OB=2BC.
点评:本题考查了切线的判定与性质,全等三角形的判定与性质.切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.
如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.