题目内容
如图所示，矩形ABCD的长为10，宽为6，点E、F将AC三等分，则△BEF的面积是________．
10
分析：E、F是AC的三等分点，则△AEB、△EFB、△FBC等底同高，因此它们的面积相等，由此可知S△BEF=
S△ABC，即可求得△BEF的面积．
解答：矩形ABCD中，∠ABC=90°，AB=10，BC=6；
∴S△ABC=
AB•BC=30．
∵E、F是AC的三等分点，
∴AE=EF=FC；
∴S△AEB=S△EFB=S△FBC=S△ABC；
∴S△BEF=S△ABC=10．
故答案为，10．
点评：本题考查矩形的性质以及三角形面积的求法，等高三角形的面积比等于底边长的比．
分析：E、F是AC的三等分点，则△AEB、△EFB、△FBC等底同高，因此它们的面积相等，由此可知S△BEF=
S△ABC，即可求得△BEF的面积．解答：矩形ABCD中，∠ABC=90°，AB=10，BC=6；
∴S△ABC=
AB•BC=30．∵E、F是AC的三等分点，
∴AE=EF=FC；
∴S△AEB=S△EFB=S△FBC=
S△ABC；∴S△BEF=
S△ABC=10．故答案为，10．
点评：本题考查矩形的性质以及三角形面积的求法，等高三角形的面积比等于底边长的比．
练习册系列答案
相关题目
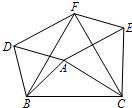18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．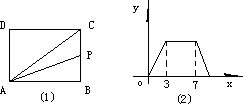
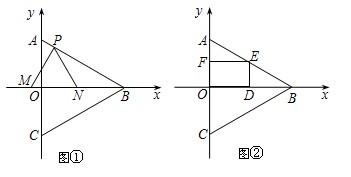
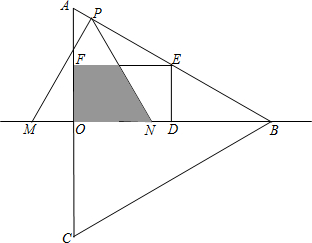边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．
（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（ ）