Question

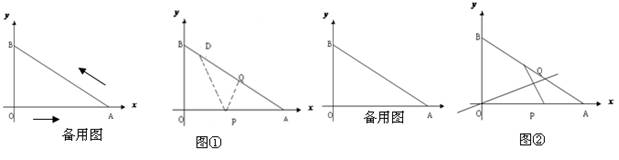
已知：如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC．
（1）求证：BG=FG；
（2）若AD=DC=2，求AB的长．

Answer 1

【答案】分析：（1）由题中可求得AE和AC所在的三角形全等，进而得到BG和FG所在三角形全等的条件；
（2）求得AF长即可求得AB长．利用等腰三角形的三线合一定理可得AF=AC=AE，进而求得一些角是30°，主要利用AD长，直角三角形勾股定理来求解．
解答：（1）证明：∵∠ABC=90°，DE⊥AC于点F，
∴∠ABC=∠AFE．（1分）
在△ABC和△AFE中，

∴△ABC≌△AFE（2分）
∴AB=AF．（3分）
连接AG，（4分）
在Rt△ABG和Rt△AFG中，

∴Rt△ABG≌Rt△AFG．（5分）
∴BG=FG；（6分）

（2）解：∵AD=DC，DF⊥AC，AF=AC=AE．（7分）
∴∠E=30°．
∵∠EAD=90°，
∴∠ADE=60°，
∴∠FAD=∠E=30°，（8分）
∴AF=．（9分）
∴AB=AF=．（10分）
点评：本题考查直角梯形、等腰三角形的性质、全等三角形的性质与判定，知识点多，综合性强．突破此题的关键在于第一问通过两次全等证Rt△ABG≌Rt△AFG，第二问求AB的长应充分利用等腰△ADC的性质得AF=AC=AE．从而得出∠E=30°．