��Ŀ����
�Ķ����ϣ�����ѧ�Ҹ�˹����ѧ����ʱ�����о�������һ�����⣺1+2+��+100=?�����о�����������һ���Խ�����l+2+3+4+5+��+n=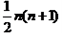 ������n���������������������о�һ�����Ƶ����⣺
������n���������������������о�һ�����Ƶ����⣺
�۲�������������ĵ�ʽ��
1 2+2
2+2 3+3
3+3 4+��+n(n+1)=?
4+��+n(n+1)=?
1 2=
2=
 (1
(1 2
2 3
3 0
0 1
1 2)
2)
2 3=
3=
 (2
(2 3
3 4
4 1
1 2
2 3)
3)
3 4=
4=
 (3
(3 4
4 5
5 2
2 3
3 4)
4)
����������ʽ�����߷ֱ���ӣ����Եõ�1 2 +2
2 +2 3 +3
3 +3 4=
4=
 3
3 4
4 5=20��
5=20��
������β��ϣ�����˼����ش�
(1)1 2 +2
2 +2 3 +3
3 +3 4+��+100
4+��+100 101=__________.
101=__________.
(2)1 ��2+2��3+3��4+��+n(n+1)=___________.
(3)1 2
2 3 +2
3 +2 3
3 4+����+n(n+1)(n+2)= ____________ ��ֻ��д�����������д�м�Ĺ��̣�
4+����+n(n+1)(n+2)= ____________ ��ֻ��д�����������д�м�Ĺ��̣�
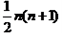 ������n���������������������о�һ�����Ƶ����⣺
������n���������������������о�һ�����Ƶ����⣺ �۲�������������ĵ�ʽ��
1
 2+2
2+2 3+3
3+3 4+��+n(n+1)=?
4+��+n(n+1)=? 1
 2=
2=
 (1
(1 2
2 3
3 0
0 1
1 2)
2) 2
 3=
3=
 (2
(2 3
3 4
4 1
1 2
2 3)
3) 3
 4=
4=
 (3
(3 4
4 5
5 2
2 3
3 4)
4) ����������ʽ�����߷ֱ���ӣ����Եõ�1
 2 +2
2 +2 3 +3
3 +3 4=
4=
 3
3 4
4 5=20��
5=20�� ������β��ϣ�����˼����ش�
(1)1
 2 +2
2 +2 3 +3
3 +3 4+��+100
4+��+100 101=__________.
101=__________. (2)1 ��2+2��3+3��4+��+n(n+1)=___________.
(3)1
 2
2 3 +2
3 +2 3
3 4+����+n(n+1)(n+2)= ____________ ��ֻ��д�����������д�м�Ĺ��̣�
4+����+n(n+1)(n+2)= ____________ ��ֻ��д�����������д�м�Ĺ��̣�(1)343400(�� )
)
(2)
(3)
 )
)(2)

(3)


��ϰ��ϵ�д�
�����Ŀ
 ������n���������������������о�һ�����Ƶ����⣺�۲�������������ĵ�ʽ��
������n���������������������о�һ�����Ƶ����⣺�۲�������������ĵ�ʽ�� ��1��2��3��0��1��2��
��1��2��3��0��1��2�� ��2��3��4��1��2��3��
��2��3��4��1��2��3�� ��3��4��5��2��3��4��
��3��4��5��2��3��4�� ��3��4��5=20
��3��4��5=20