题目内容
 如图,已知△ABC中,AC+BC=16,AO、BO分别是∠CAB、∠ABC的角平分线.MN经过点O,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为________.
如图,已知△ABC中,AC+BC=16,AO、BO分别是∠CAB、∠ABC的角平分线.MN经过点O,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为________.
16
分析:根据AO、BO分别是角平分线和MN∥BA,求证△AON和△BOM为等腰三角形,再根据AC+BC=16,利用等量代换即可求出△CMN的周长.
解答:AO、BO分别是角平分线,
∴∠OAN=∠BAO,∠ABO=∠OBM,
∵MN∥BA,
∴∠AON=∠BAO,∠MOB=∠ABO,
∴AN=ON,BM=OM,即△AON和△BOM为等腰三角形,
∵MN=MO+ON,AC+BC=16,
∴△CMN的周长=MN+MC+NC=AC+BC=16.
故答案为:16.
点评:此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握,此题关键是求证△AON和△BOM为等腰三角形.
分析:根据AO、BO分别是角平分线和MN∥BA,求证△AON和△BOM为等腰三角形,再根据AC+BC=16,利用等量代换即可求出△CMN的周长.
解答:AO、BO分别是角平分线,
∴∠OAN=∠BAO,∠ABO=∠OBM,
∵MN∥BA,
∴∠AON=∠BAO,∠MOB=∠ABO,
∴AN=ON,BM=OM,即△AON和△BOM为等腰三角形,
∵MN=MO+ON,AC+BC=16,
∴△CMN的周长=MN+MC+NC=AC+BC=16.
故答案为:16.
点评:此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握,此题关键是求证△AON和△BOM为等腰三角形.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.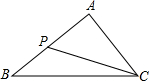 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )