Question

【题目】如图，抛物线y＝ax2+bx+4交y轴于点A，并经过B（4，4）和C（6，0）两点，点D的坐标为（4，0），连接AD，BC，点F从点O出发，以每秒1个单位长度的速度沿线段OC方向运动，到达点C后停止运动：点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动，当点F停止时点M也停止运动．设点F的运动时间为t秒，过点F作AB的垂线EF交直线AB于点E，交AD于点H．

（1）求抛物线的解析式；

（2）以线段EH为斜边向右作等腰直角△EHG，当点G落在第一象限内的抛物线上时，求出t的值；

（3）设△EFM与四边形ADCB重合时的面积为S，请直接写出S与t的函数关系式与相应的自变量t的取值范围．

Answer 1

【答案】（1）y＝﹣x2+x+4；（2）t＝；（3）S＝．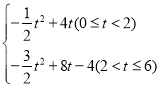

【解析】

（1）由题意得：函数的对称轴为：x＝2，则函数与x轴的另外一个交点坐标为（2，0），则函数的表达式为：y＝a（x＋2）（x6）＝a（x24x12），即可求解；

（2）求出点G（，），将点G的坐标代入表达式，即可求解；

（3）分0＜t≤2、2＜t≤6两种情况分别求解即可．

（1）由题意得：函数的对称轴为：x＝2，则函数与x轴的另外一个交点坐标为（﹣2，0），

则函数的表达式为：y＝a（x+2）（x﹣6）＝a（x2﹣4x﹣12），

则﹣12a＝4，解得：a＝﹣，

故抛物线的表达式为：y＝﹣x2+x+4；

（2）将点A、D的坐标代入一次函数表达式并解得：

直线AD的表达式为：y＝﹣x+4，

则点E、F的坐标分别为：（t，4）、（t，0），

则点H（t，4﹣t），则点G（，4﹣t），

将点G的坐标代入表达式得：4﹣t＝﹣·（）2+·+4，

解得：t＝；

（3）点M（t+4，0），点E（t，4）、点F（t，0），

①当0＜t≤2时，设EF交AD于点N（t，4﹣t），

S＝S△EFM﹣S△FND＝8﹣×（4﹣t）2＝﹣t2+4t，

②2＜t≤6时，

设直线EM交BC于点R，EF交AD于点K（t，4﹣t），

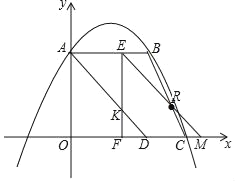
同理可得：直线ME的表达式为：y＝﹣x+t+4，

直线BC的表达式为：y＝﹣2x+12，

联立上述两式并解得：x＝8﹣t，

故点R（8﹣t，2t﹣4），

S＝S△EFM﹣S△RCM﹣S△KFD＝4×4﹣（t+4﹣6）（2t﹣4）﹣×（4﹣t）2＝﹣t2+8t﹣4；

故S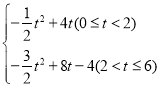＝．