题目内容
一个三角形零件中，AB=AC=13，BC=10，因安装的需要，工人师傅在BC和AC上凿出两个孔M和N，点M是BC中点，MN⊥AC于点N，则MN=
．
| 60 |
| 13 |
| 60 |
| 13 |
分析：首先利用等腰三角形的性质和勾股定理求得AM的长，然后利用等积法求得线段MN的长即可．
解答：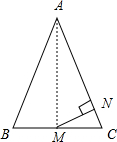
解：∵AB=AC=13，BC=10，点M是BC中点，
∴AM⊥BC，BM=MC=5，
∴根据勾股定理得：AM=12
∵MN⊥AC于点N，
∴MN=
=
=
故答案为：
解：∵AB=AC=13，BC=10，点M是BC中点，∴AM⊥BC，BM=MC=5，
∴根据勾股定理得：AM=12
∵MN⊥AC于点N，
∴MN=
| AM•MC |
| AC |
| 12×5 |
| 13 |
| 60 |
| 13 |
故答案为：
| 60 |
| 13 |
点评：本题考查了勾股定理的应用，根据题意正确的作出图形是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
