Question

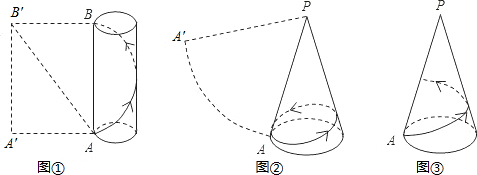
沿一条母线将圆锥侧面剪开并展平，得到圆锥的侧面展开图是一个    ．若设圆锥的母线长为l，底面圆的半径为r，那么这个扇形的半径为    ，扇形的弧长为    ，因此圆锥的侧面积为    ，圆锥的全面积为    ．

Answer 1

【答案】分析：根据圆锥的展开图为扇形，结合弧长公式、圆周长的求解公式、面积的求解公式，圆锥侧面积的求解公式可得出答案．
解答：解：圆锥的侧面展开图是一个扇形，扇形的半径等于圆锥的母线长，扇形的弧长等于圆锥的底面圆周长，
故可得，这个扇形的半径为l，扇形的弧长为2πr，
圆锥的侧面积为S_侧=•2πr•l=πrl；
圆锥的全面积为圆锥的全面积：S_全=S_底+S_侧=πr²+πrl．
故答案为：扇形、l、2πr、πrl、πr²+πrl．
点评：此题考查了圆锥的计算，解答本题的关键是掌握圆锥侧面展开图是个扇形，要熟练掌握扇形与圆锥之间的联系，难度一般．