��Ŀ����
����Ŀ��Ϊ�ٿ������˶��ᣬѧУ��������һ�����������������3�������2��������420Ԫ������2�������4��������440Ԫ.
��1�������������ĵ��ۣ�
��2������ʵ����Ҫ��ѧУ�����������������100�������й����������������������������![]() ��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��ѧУ�����ڹ������������������ʽ����Ϊ8000Ԫ.�����м��ֹ�����
��3������������![]() ����ѧУ�������������������ܷ���Ϊ
����ѧУ�������������������ܷ���Ϊ![]() Ԫ���ڣ�2���������£������ַ�����ʹ
Ԫ���ڣ�2���������£������ַ�����ʹ![]() ��С�������
��С�������![]() ����Сֵ.
����Сֵ.
���𰸡���1������Ϊ100Ԫ������Ϊ60Ԫ����2����11�ֹ���.����3����������![]() ��СΪ7600Ԫ.
��СΪ7600Ԫ.
��������
��1����ÿ������xԪ��ÿ������yԪ�����������鼴�ɽ�����⣻
��2���蹺������m��������100-m��������������ʽ�飬�������⼴�ɣ�
��3������һ�κ���������һ�κ��������ʼ��ɽ������.
��1����ÿ������xԪ��ÿ������yԪ�������⣬�ã�
![]()
���![]()
������Ϊ100Ԫ������Ϊ60Ԫ.
��2���蹺������m��������100-m������������ɵã�
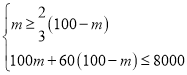
��ã�40��m��50��
��m��������
��m=40��41��42��43��44��45��46��47��48��49��50��
���11�ֹ�����
��3��������ɵ�y=100x+60��100-x��=40x+6000��40��x��50��
��k=40��0
��y��x�����������
�൱x=40ʱ��y����Сֵ��y��С=40��40+6000=7600��Ԫ��
���Ե�x=40ʱ��y����СֵΪ7600Ԫ��

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�