题目内容
如图，四个4×4的正方形网格（每个网格中的小正方形边长都是1），每个网格中均有一个“格点三角形”（三角形顶点在小正方形的顶点上），是相似三角形的为（ ）
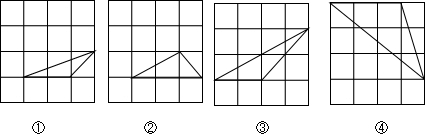
| A、①③ | B、①② | C、②③ | D、②④ |
分析：可分别求出三角形的边长，根据对应边成比例，三角形互为相似三角形可进行判断．
解答：解：第一个三角形的边长分别为：
，2，
．
第二个三角形的边长分别为：
，
，3．
第三个三角形的边长分别为：2，2
，2
．
第四个三角形的边长分别为：3，
，4
．
对应边成比例的是①③．
故选A．
| 2 |
| 10 |
第二个三角形的边长分别为：
| 2 |
| 5 |
第三个三角形的边长分别为：2，2
| 2 |
| 5 |
第四个三角形的边长分别为：3，
| 17 |
| 2 |
对应边成比例的是①③．
故选A．
点评：本题考查相似三角形的判定定理，三边对应成比例，这两个三角形互为相似三角形．
练习册系列答案
相关题目
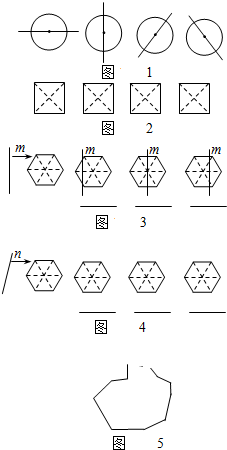（2013•池州一模）我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分（如图1）．
如图，5个全等的正六边形A、B、C、D、E，请仔细观察A、B、C、D四个图案，其中与E图案也完全相同的是
[ ]
|
A． |
B． |
|
C． |
D． |
|
E． |
交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2，两条抛物线相交于点C．