Question

【题目】如图，在x轴上方，∠BOA=90°且其两边分别与反比例函数y=﹣ 、y= 的图象交于B、A两点，则∠OAB的正切值为（）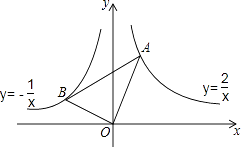
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图，分别过点A、B作AN⊥x轴、BM⊥x轴； ∵∠AOB=90°，
∴∠BOM+∠AON=∠AON+∠OAN=90°，
∴∠BOM=∠OAN，
∵∠BMO=∠ANO=90°，
∴△BOM∽△OAN，
∴ = ；
设B（﹣m， ），A（n， ），
则BM= ，AN= ，OM=m，ON=n，
∴mn= ，mn= ；
∵∠AOB=90°，
∴tan∠OAB= ①；
∵△BOM∽△OAN，
∴ = = = ②，
由①②知tan∠OAB= ，
故选B．

【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．