Question

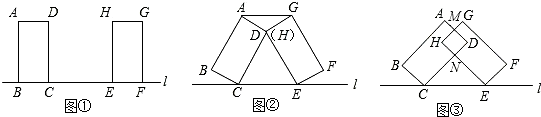
两个长为2，宽为1的矩形ABCD和矩形EFGH如图1所示摆放在直线l上，DE=2，将矩形ABCD绕点D顺时针旋转α角（0°＜α＜90°），将矩形EFGH绕点E逆时针旋转相同的角度．在旋转的过程中，利用图2思考：当矩形ABCD和矩形EFGH重合部分为正方形时，α=________°．

Answer 1

45
分析：由四边形MFNC为正方形，而矩形ABCD绕点D顺时针旋转和矩形EFGH绕点E逆时针旋转相同的角度．得到NF=NC，∠FNC=90°，则∠DNE=90°，ND=NE，得到∠NDE=∠NED=45°，所以∠1=180°-90°-45°=45°，即α=45°．
解答：∵四边形MFNC为正方形，而矩形ABCD绕点D顺时针旋转和矩形EFGH绕点E逆时针旋转相同的角度，
∴NF=NC，∠FNC=90°，
∴∠DNE=90°，ND=NE，
∴∠NDE=∠NED=45°，
∴∠1=180°-90°-45°=45°，
∴α=45°．
故答案是：45．
点评：本题考查了旋转的性质：旋转前后两个图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段的夹角等于旋转角．也考查了矩形和等腰三角形的性质．