题目内容
下列多项式相乘，能用平方差公式的是（ ）
| A、（x-y）（y-x） |
| B、（2x-3y）（-2x+3y） |
| C、（x-y-z）（-x+y+z） |
| D、（x-3y）（-x-3y） |
考点：平方差公式
专题：
分析：根据平方差公式：两个数的和乘两个数的差，等于两个数的平方差，字母表示为：（a+b）（a-b）=a2-b2，找出整式中的a和b，进行判定即可．
解答：解：A、（x-y）（y-x），不符合平方差公式的特点，故选项A错误；
B、（2x-3y）（-2x+3y），不符合平方差公式的特点，故选项B错误；
C、（x-y-z）（-x+y+z）=[x-（y+z）][（y+z）-x]不符合平方差公式的特点，故选项C错误；
D、（x-3y）（-x-3y）=（-3y+x）（-3y-x），符合平方差公式的特点，故D选项正确．
故选：D．
B、（2x-3y）（-2x+3y），不符合平方差公式的特点，故选项B错误；
C、（x-y-z）（-x+y+z）=[x-（y+z）][（y+z）-x]不符合平方差公式的特点，故选项C错误；
D、（x-3y）（-x-3y）=（-3y+x）（-3y-x），符合平方差公式的特点，故D选项正确．
故选：D．
点评：此题考查平方差公式，注意抓住整式的特点，灵活变形．
练习册系列答案
相关题目
如图，CD是⊙O的直径，CD=10，点A在⊙O上，∠ACD=30°，B为
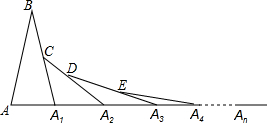如图，在△ABA1中，∠B=20°，∠BAA1=∠BA1A，在A1B上取一点C，延长AA1到A2，使得∠A1CA2=∠A1A2C；在A2C上取一点D，延长A1A2到A5，使得∠A2DA3=∠A2A3D，…，按此做法进行下去，∠An的度数为