题目内容
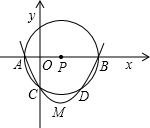 (1998•黄冈)如图,直角坐标系中,O为坐标原点,A点坐标为(-3,0),B点坐标为(12,0),以AB为直径作⊙P与y轴的负半轴交于点C.抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M点.
(1998•黄冈)如图,直角坐标系中,O为坐标原点,A点坐标为(-3,0),B点坐标为(12,0),以AB为直径作⊙P与y轴的负半轴交于点C.抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M点.(1)求此抛物线的解析式;
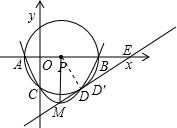
(2)设点D是抛物线与⊙P的第四个交点(除A、B、C三点以外),求直线MD的解析式;
(3)判定(2)中的直线MD与⊙P的位置关系,并说明理由.
分析:(1)由已知条件求出C点的坐标,再把A,B,C点的坐标代入即可求出此抛物线的解析式;
(2)由圆的对称性和抛物线的对称性可知C和D关于直线PM对称,由C的坐标即可求出D点的坐标,根据抛物线的解析式可求出M的坐标,设直线MD的解析式y=kx+b,把M,D的坐标代入求出k和b的值即可;
(3)直线MD与⊙P的位置关系设直线DM和x轴交于E,连接PM则PM⊥OE,过P作PD′⊥ME于D′,设y=0,则y=
x-
=0,则可求出OE的长,根据勾股定理求出ME,在根据三角形的面积为定值可求出PD′的长,和圆P的半径比较大小即可判定(2)中的直线MD与⊙P的位置关系.
(2)由圆的对称性和抛物线的对称性可知C和D关于直线PM对称,由C的坐标即可求出D点的坐标,根据抛物线的解析式可求出M的坐标,设直线MD的解析式y=kx+b,把M,D的坐标代入求出k和b的值即可;
(3)直线MD与⊙P的位置关系设直线DM和x轴交于E,连接PM则PM⊥OE,过P作PD′⊥ME于D′,设y=0,则y=
| 3 |
| 4 |
| 51 |
| 4 |
解答:解:(1)连接PC,
∵A点坐标为(-3,0),B点坐标为(12,0),
∴AB=15,
∴AP=BP=PC=7.5,
∴OP=7.5-3=4.5,
∴OC=
=6,
∴C(0,-6)
把A(-3,0),B(12,0),C(0,6)代入y=ax2+bx+c得:
,
解得:
,
∴y=
x2-
x-6;
(2)∵y=
x2-
x-6=
(x-
)x2-
;
∴M(
,-
),
∵P是圆的圆心,
∴PM是圆的对称轴,PM是抛物线的对称轴,
∵C(0,-6),
∴D(9,-6),
设直线MD的解析式y=kx+b,把D(9,-6)和M(
,-
)代入得:
,
解得:
,
∴y=
x-
;
(3)设直线DM和x轴交于E,连接PM,则PM⊥OE,过P作PD′⊥ME于D′,
设y=0,则y=
x-
=0,
∴x=17,
∴OE=17,∴E(17,0),
∴PE=17-4.5=12.5,
∵PM=
,
∴ME=
=
,
∵
PM•PE=
PD′•EM,
∴PD′=
=7.5,
∴PD′等于圆的半径,
∴直线MD与⊙P的位置关系是相切.
∵A点坐标为(-3,0),B点坐标为(12,0),

∴AB=15,
∴AP=BP=PC=7.5,
∴OP=7.5-3=4.5,
∴OC=
| PC2-OP2 |
∴C(0,-6)
把A(-3,0),B(12,0),C(0,6)代入y=ax2+bx+c得:
|
解得:
|
∴y=
| 1 |
| 6 |
| 3 |
| 2 |
(2)∵y=
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 6 |
| 9 |
| 2 |
| 75 |
| 8 |
∴M(
| 9 |
| 2 |
| 75 |
| 8 |
∵P是圆的圆心,
∴PM是圆的对称轴,PM是抛物线的对称轴,
∵C(0,-6),
∴D(9,-6),
设直线MD的解析式y=kx+b,把D(9,-6)和M(
| 9 |
| 2 |
| 75 |
| 8 |
|
解得:
|

∴y=
| 3 |
| 4 |
| 51 |
| 4 |
(3)设直线DM和x轴交于E,连接PM,则PM⊥OE,过P作PD′⊥ME于D′,
设y=0,则y=
| 3 |
| 4 |
| 51 |
| 4 |
∴x=17,
∴OE=17,∴E(17,0),
∴PE=17-4.5=12.5,
∵PM=
| 75 |
| 8 |
∴ME=
| PE2+PM2 |
| 125 |
| 8 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴PD′=
| 15 |
| 2 |
∴PD′等于圆的半径,
∴直线MD与⊙P的位置关系是相切.
点评:本题考查了用待定系数法求一次函数和二次函数的解析式、二次函数的性质、顶点坐标的求法、一次函数和坐标轴的交点、圆的性质、切线的判定以及勾股定理的运用,题目的综合性很强,难度不小.

练习册系列答案
相关题目
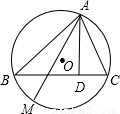
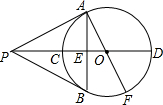 (1998•黄冈)如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,下列结论:①∠ABP=∠AOP;②
(1998•黄冈)如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,下列结论:①∠ABP=∠AOP;②
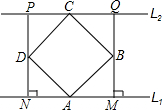 (1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.
(1998•黄冈)如图,已知四边形ABCD是正方形,分别过A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、ND分别交l2于Q、P.求证:四边形PQMN是正方形.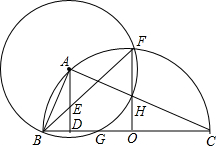 (1998•黄冈)如图,⊙O是△ABC的外接圆,BC是直径,以顶点A为圆心,AB长为半径的圆交⊙O于F点,交BC于G点(AB<OB).AD⊥BC于D,AD与BF交于E点,OF交⊙A于H点.求证:
(1998•黄冈)如图,⊙O是△ABC的外接圆,BC是直径,以顶点A为圆心,AB长为半径的圆交⊙O于F点,交BC于G点(AB<OB).AD⊥BC于D,AD与BF交于E点,OF交⊙A于H点.求证: