题目内容
如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.

考点:
正方形的性质;二次函数的最值;全等三角形的判定与性质;勾股定理;相似三角形的判定与性质.
分析:
(1)由已知∠AEB=∠BFC=90°,AB=BC,结合∠ABE=∠BCF,证明△ABE≌△BCF,可得AE=BF,于是AE2+CF2=BF2+CF2=BC2=16为常数;
(2)设AP=x,则PD=4﹣x,由已知∠DPM=∠PAE=∠ABP,△PDM∽△BAP,列出关于x的一元二次函数,求出DM的最大值.
解答:
解:(1)由已知∠AEB=∠BFC=90°,AB=BC,
又∵∠ABE+∠FBC=∠BCF+∠FBC,
∴∠ABE=∠BCF,
∵在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF,
∴AE2+CF2=BF2+CF2=BC2=16为常数;
(2)设AP=x,则PD=4﹣x,
由已知∠DPM=∠PAE=∠ABP,
∴△PDM∽△BAP,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴DM=![]() =x﹣
=x﹣![]() x2,
x2,
当x=2时,DM有最大值为1.
点评:
本题主要考查正方形的性质等知识点,解答本题的关键是熟练掌握全等三角形的判定定理以及三角形相似等知识,此题有一定的难度,是一道不错的中考试题.

练习册系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以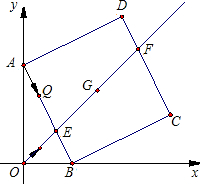 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.