题目内容
已知E、F分别在正方形ABCD的边BC、CD上的点，AE、AF分别与对角线BD相交于M、N，若∠EAF=50°，则∠CME+∠CNF=（ ）A．100°
B．90°
C．110°
D．120°
【答案】分析：先根据三角形内角和外角的关系，建立起，∠1、∠2和∠3、∠4、∠5、∠6的关系，再根据全等，找出相等的角．
解答：
解：∵∠3+∠5=∠1，∠4+∠6=∠2
∴（∠3+∠4）+（∠5+∠6）=∠1+∠2
∴∠1+∠2=50°+（∠5+∠6）
∵AD=CD，∠ADN=∠CDN，DN=DN
∴△ADN≌△CDN
∴AN=CN
同理AM=CM
∵MN=MN
∴△AMN≌△CMN
∴∠5+∠6=∠3+∠4=50°
∴∠CME+∠CNF=∠1+∠2=50°+（∠5+∠6）=50°+50°=100°
故选A．
点评：此题主要考查正方形对角线相互垂直平分相等的性质及全等三角形的判定等知识的综合运用．
解答：
解：∵∠3+∠5=∠1，∠4+∠6=∠2∴（∠3+∠4）+（∠5+∠6）=∠1+∠2
∴∠1+∠2=50°+（∠5+∠6）
∵AD=CD，∠ADN=∠CDN，DN=DN
∴△ADN≌△CDN
∴AN=CN
同理AM=CM
∵MN=MN
∴△AMN≌△CMN
∴∠5+∠6=∠3+∠4=50°
∴∠CME+∠CNF=∠1+∠2=50°+（∠5+∠6）=50°+50°=100°
故选A．
点评：此题主要考查正方形对角线相互垂直平分相等的性质及全等三角形的判定等知识的综合运用．
练习册系列答案
全能练考卷系列答案
相关题目
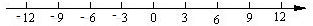
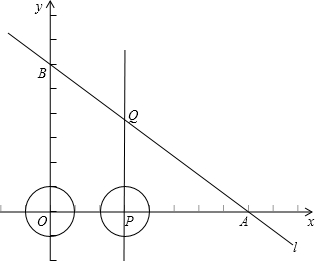轴分别交于点A、B．
