题目内容
【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为 . 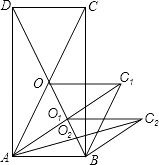
【答案】![]()
【解析】解:∵四边形ABCD是矩形,
∴AO=CO,BO=DO,DC∥AB,DC=AB,
∴S△ADC=S△ABC= ![]() S矩形ABCD=
S矩形ABCD= ![]() ×20=10,
×20=10,
∴S△AOB=S△BCO= ![]() S△ABC=
S△ABC= ![]() ×10=5,
×10=5,
∴S ![]() =
= ![]() S△AOB=
S△AOB= ![]() ×5=
×5= ![]() ,
,
∴S ![]() =
= ![]() S
S ![]() =
= ![]() ,
,
S ![]() =
= ![]() S
S ![]() =
= ![]() ,
,
S ![]() =
= ![]() S
S ![]() =
= ![]() ,
,
∴S ![]() =2S
=2S ![]() =2×
=2× ![]() =
= ![]()
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目
