题目内容
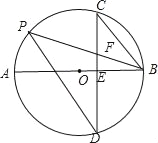
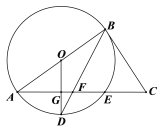
【题目】如图,在⊙O中,AB是⊙O的直径,AE是弦,OG⊥AE于点G,交⊙O 于点D,连结BD交AE于点F,延长AE至点C,连结BC.
(1)当BC=FC时,证明:BC是⊙O的切线;
(2)已知⊙O的半径![]() ,当tanA=
,当tanA=![]() ,求GF的长.
,求GF的长.
【答案】(1)见解析;(2)1
【解析】
(1)由OD⊥AE可知∠D+∠GFD=90°,由等腰三角形的性质可得∠BFC=∠FBC,∠OBD=∠D,从而可证∠OBC=90°;
(2) 连接 BE,在Rt△AOG中,可求出OG= 3, AG=4,由垂径定理得GE= AG=4,然后通过证明△FGD∽△FEB,可求出GF的长.
(1)证明:∵OD⊥AE.
∴∠D+∠GFD=90°.
∵BC=FC,
∴∠BFC=∠FBC.
∵∠BFC=∠GFD,
∴∠GFD=∠FBC.
∵OB=OD,
∴∠OBD=∠D.
∴∠OBD+∠CBF=∠D+∠GFD=90°.
即∠OBC=90°.
∴BC是![]() 的切线.
的切线.
(2) 连接 BE,

∵⊙O半径![]() ,tanA=
,tanA=![]() ,
,
∴sinA=![]() ,cosA=
,cosA=![]() .
.
∴在Rt△AOG中,OG=OA sinA=5×![]() =3, AG=OA cosA=5×
=3, AG=OA cosA=5×![]() =4=GE.
=4=GE.
∴GD=OD-OG=5-3=2.
∵OG⊥AE,
∴AG=GE.
∴OG是△ABE的中位线,
∴BE=2OG=6,BE∥OD.
∴∠D=∠FBE,∠BEF=∠FGD.
∴△FGD∽△FEB.
∴![]() .
.
∴![]() .
.
∴GF=1.

练习册系列答案
相关题目
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是 ;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.