题目内容
解方程组：
．
解：已知
由①得x=y+2③
把③代入②得，
（y+2）2+（y+2）y=12
即y2+3y-4=0
解得y1=-4，y2=1
将y1=-4代入③得x1=-2
将y2=1代入③得x2=3
∴原方程组的解为
，
．
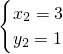分析：对方程x-y=2，移项得x=y+2，将其代入方程x2+xy=12，把它化为关于y的方程，然后对其进行合并同类型解出y值，再把y值代入方程x-y=2，求出x，从而求出方程组的解．
点评：解高次方程的一般解题方法是把简单的方程进行化简代入比较复杂的高次方程，把它化为关于x或y的方程后，再进行求解，这样有利于减少计算量．
由①得x=y+2③
把③代入②得，
（y+2）2+（y+2）y=12
即y2+3y-4=0
解得y1=-4，y2=1
将y1=-4代入③得x1=-2
将y2=1代入③得x2=3
∴原方程组的解为
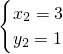，．分析：对方程x-y=2，移项得x=y+2，将其代入方程x2+xy=12，把它化为关于y的方程，然后对其进行合并同类型解出y值，再把y值代入方程x-y=2，求出x，从而求出方程组的解．
点评：解高次方程的一般解题方法是把简单的方程进行化简代入比较复杂的高次方程，把它化为关于x或y的方程后，再进行求解，这样有利于减少计算量．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
（1）解方程组：